La freccia del tempo
.
La freccia del tempo
di Alberto Abbondandolo
Navigando per il sito di XlaTangente ci si può imbattere in due video curiosi. Il primo (in alto quattro fotogrammi, in basso l'intero video) mostra un pendolo piuttosto particolare: ha la forma di un cavaliere, con vari snodi in corrispondenza delle articolazioni dell'uomo e del cavallo. Il pendolo non è appeso, ma oscilla in equilibrio sulla punta degli zoccoli posteriori del cavallo, poggiati su una piattaforma. Un contrappeso bilancia perfettamente il peso di cavallo e cavaliere permettendo oscillazioni piuttosto ampie che producono un bell'effetto di cavaliere al galoppo.
Nel secondo video (qui sotto sei fotogrammi, più giù l'intero video) vediamo un liquido violaceo, abbastanza uniforme. Il liquido viene mescolato lentamente da un cucchiaio, ma l'effetto è piuttosto strano: man mano che il cucchiaio mescola si creano zone più blu, zone più rosse e zone quasi trasparenti. Sembra che il blu e il rosso vogliano separarsi in un processo che continua anche dopo che il cucchiaio viene tolto: alla fine si vedono una massa rossa e una massa blu completamente separate, in sospensione in un liquido trasparente.
Che razza di mistura potrà mai avere un tale comportamento?
Una didascalia ci informa che i due video hanno una cosa in comune. Un click del mouse e il mistero è svelato: entrambi i video sono in reverse, ossia sono stati rimontati al contrario. Vedendo il secondo video forse l'avevamo sospettato: la strana mistura altro non è che comunissima acqua in cui vengono fatte cadere una goccia di inchiostro blu e una di inchiostro rosso, successivamente mescolate dal cucchiaio. Capire che il primo video aveva subìto la stessa inversione era invece quasi impossibile, se non guardando attentamente cosa accade alle lancette di un orologio, che forse non avevamo nemmeno notato, posto poco sotto gli zoccoli posteriori del cavallo (si veda il video qui sotto).
Ma il sito di XlaTangente non è l'unico ad ospitare curiosità di questo tipo. Fino a qualche mese fa su YouTube si poteva vedere un video - adesso rimosso dal sito web - in cui il regista e sceneggiatore Michel Gondry ricomponeva un cubo di Rubik con i piedi, senza nemmeno prestarvi troppa attenzione. Un altro utente di Youtube si è accorto del trucco: Michel Gondry è partito da un cubo di Rubik già composto, si è fatto riprendere mentre lo scomponeva con i piedi, infine ha rimontato il video in reverse. Il regista ha cercato di camuffare l'inversione inserendo sullo sfondo una persona che cammina all'indietro - quindi in avanti nel video invertito - ma il suo modo innaturale di camminare rivela il trucco (si veda il video qui sotto).
Se sullo schermo invertire la freccia del tempo è cosa facile, sulla pagina scritta non è comunque impossibile: nel romanzo intitolato non a caso The time arrow Martin Amis mantiene questa inversione dall'inizio alla fine della narrazione.
Ecco come il protagonista racconta l'esperienza di un pasto in reverse:
Eating is unattractive too. [...] You select a soiled dish, collect some scraps from the garbage, and settle down for a short wait. Various items get gulped up into my mouth, and after a skilful massage with tongue and teeth I transfer them to the plate for additional sculpture with knife and fork and spoon. That bit's quite therapeutic at least, unless you're having soup or something, which can be a real sentence. Next you face the laborious business of cooling, of reassembly, of storage, before the return of these foodstuffs to the Superette, where, admittedly, I am promptly and generously reimbursed for my pains. Then you tool down the aisles with trolley or basket, returning each can or packet to its rightful place [1].
Ma torniamo ai due video del sito di XlaTangente. Abbiamo scoperto che i due video sono montati al contrario. Dunque è tutto chiarito? Beh, non proprio: resta il fatto che le leggi della meccanica, che regolano sia il moto del cavaliere sia quello delle particelle di inchiostro nell'acqua, sono perfettamente reversibili. Ciò significa che quel che vediamo nei due video in reverse non viola alcuna legge della fisica. Perché allora non vediamo mai una soluzione di acqua e inchiostro comportarsi come quella del secondo video? Anzi, come mai quasi tutti i fenomeni che ci circondano, da un piatto che cade e si rompe a un palloncino che scoppia alla stessa vita degli esseri umani, mostrano un comportamento irreversibile? E cosa differenzia quei sistemi che, come il cavaliere o il sistema solare, sembrano interpretare alla lettera la reversibilità delle leggi fisiche?
Negli ultimi trent'anni del diciannovesimo secolo James Maxwell, William Thomson, e soprattutto il fisico austriaco Ludwig Boltzmann hanno risposto a queste domande. Nelle pagine che seguono descriveremo le loro idee, insieme ad alcuni degli sviluppi più recenti.
Le leggi della meccanica sono reversibili
Conosciamo tutti l'equazione fondamentale della meccanica, la famosa equazione di Newton
F = m a.
L'equazione di Newton ci dice che l'accelerazione [2] a di un corpo - che pensiamo come un punto materiale privo di dimensioni - è pari alla risultante F delle forze che agiscono su di esso divisa per sua la massa m. Il fatto che in questa equazione compaia l'accelerazione ma non la velocità implica che l'equazione di Newton sia reversibile.
Immaginiamo ad esempio un Eurostar Roma-Milano che, superata da poco Firenze, acceleri su un rettilineo. In che direzione puntano la sua velocità e la sua accelerazione? Entrambe verso nord, ovviamente. Immaginiamo ora di filmare questo tratto di corsa del treno e di rivedere il video montato al contrario. In che direzione puntano adesso velocità ed accelerazione? Allo spettatore sembrerà che il treno proceda in direzione nord-sud e che sia frenando. Quindi la velocità adesso punta verso sud, mentre l'accelerazione continua a puntare verso nord (una frenata corrisponde ad un'accelerazione in direzione contraria al senso di marcia). La conclusione è che invertendo la freccia del tempo l'accelerazione non cambia [3]. Dato che né la forza che agisce su un corpo né tantomeno la sua massa cambiano invertendo la freccia del tempo, concludiamo che l'equazione di Newton è invariante per inversione temporale.
Per comprendere meglio cosa comporti questo tipo di invarianza abbiamo bisogno di capire come l'equazione di Newton determini il moto di un corpo. L'accelerazione a(t) all'istante t misura quanto rapidamente stia variando la velocità v(t), la quale a sua volta misura quanto rapidamente stia variando la posizione q(t). La forza F che agisce sul corpo dipende in generale dalla sua posizione: la forza di gravità esercitata dal nostro pianeta dipende dalla distanza dal centro della terra, la forza di richiamo di una molla dipende dl suo allungamento, la forza che attrae o respinge due cariche elettriche dipende dalla loro mutua distanza [4].
Ricapitolando: l'equazione di Newton ci dice che l'accelerazione è proporzionale alla forza, che dipende dalla posizione, la cui variazione a sua volta determina l'accelerazione. Sembra il classico gatto che si morde la coda. Relazioni di questo tipo si dicono equazioni differenziali. Fortunatamente tout se tient: un importante teorema ci assicura che, fissate arbitrariamente posizione e velocità iniziale q(0) e v(0), esiste ed è unica una traiettoria q(t) che risolve l'equazione differenziale per tutti i tempi - passati e futuri - e rispetta le condizioni iniziali [5].
Se i corpi sono molti il numero delle equazioni aumenta ma la loro forma resta invariata: in presenza di N corpi abbiamo bisogno di n=3N numeri, che indichiamo con q1, q2, ..., qn, per determinare le posizioni, e di altrettanti numeri, indicati con v1, v2, ..., vn, per determinare le velocità. Il numero n si dice numero dei gradi di libertà del sistema. L'evoluzione di quest'ultimo è determinata univocamente da un sistema di n equazioni differenziali e da n posizioni e n velocità iniziali.
Rientrano in questo formalismo tanto il pendolo a forma di cavaliere (anche se qui non si tratta di punti materiali, questo è un sistema con sei gradi di libertà e la forza è quella gravitazionale), quanto la soluzione di acqua e inchiostro (qui i gradi di libertà sono tantissimi, tre per ogni molecola d'acqua o di inchiostro, se le consideriamo puntiformi, ancora di più se teniamo conto anche della struttura tridimensionale delle molecole, in ogni caso un numero dell'ordine di 1024, un 1 seguito da 24 zeri). Infatti qualunque sistema fisico [6] può essere descritto dalle equazioni di Newton, fatto che Laplace sintetizzava in una frase celebre, divenuta emblema del determinismo:
Un intelletto che ad un dato istante conoscesse tutte le forze che animano la Natura e la situazione di ogni singolo essere che questa comprende, se questo stesso intelletto fosse sufficientemente vasto per sottoporre ad analisi questi dati, potrebbe abbracciare in un'unica formula tanto il moto dei più corpi dell'universo, quanto quello dell'atomo più leggero: per tale intelletto nulla sarebbe incerto, e il futuro, così come il passato, sarebbero presenti davanti ai suoi occhi [7].
La reversibilità delle equazioni di Newton può quindi essere letta nel modo seguente: se le n funzioni q1(t), q2(t), ..., qn(t) rappresentano una possibile evoluzione di un certo sistema fisico, ossia costituiscono una soluzione del corrispondente sistema di equazioni differenziali, allora l'evoluzione in reverse, descritta dalle n funzioni q1(−t), q2(−t), ..., qn(−t), è ancora un'evoluzione possibile, in quanto risolve il medesimo sistema di equazioni con le stesse posizioni iniziali e le velocità iniziali invertite. In altre parole, se potessimo intervenire sulle singole molecole della soluzione di acqua e inchiostro ormai mescolata in modo da invertirne istantaneamente tutte le velocità, vedremmo l'inchiostro rosso e quello blu separarsi, proprio come nel video in reverse.
Risolvere le equazioni di Newton
Prima di vedere come Boltzmann ha spiegato questo apparente paradosso, dobbiamo chiarire cosa si intenda per risolvere le equazioni di Newton. Tranne che in casi molto particolari - pochissimi gradi di libertà, forze dall'espressione semplice - non è possibile risolvere in maniera esatta [8] un sistema di equazioni differenziali. Né sarebbe particolarmente utile: se vogliamo capire il comportamento globale del sistema non ci basta conoscere la sua evoluzione a partire da una data condizione iniziale, ma vogliamo tenere in qualche modo conto di tutte le possibili condizioni iniziali. Per questo motivo è utile pensare alle equazioni di Newton in termini geometrici, introducendo lo spazio delle fasi. Uno stato del sistema è dato dai 2n numeri q1, q2, ..., qn, v1, v2, ..., vn, le posizioni e velocità di tutte le componenti del sistema, che come abbiamo visto determinano completamente l'evoluzione passata e futura. Così come due numeri individuano un punto sul piano bidimensionale e tre numeri ne individuano uno nello spazio tridimensionale, i 2n numeri ( q1, q2, ..., qn, v1, v2, ..., vn) possono essere pensati come coordinate di un punto in uno spazio con 2n dimensioni, lo spazio delle fasi. Quindi lo spazio delle fasi è lo spazio di tutti i possibili stati del sistema e la sua dimensione è pari al doppio del numero dei gradi di libertà. L'evoluzione del sistema può adesso essere pensata come al moto di un punto nello spazio delle fasi.
Le equazioni di Newton determinano una famiglia di trasformazioni Tt, al variare di t tra tutti i numeri reali, dello spazio delle fasi in sé: l'immagine dello stato x tramite la trasformazione Tt è lo stato Tt(x) che si ottiene risolvendo le equazioni di Newton a partire dalla condizione iniziale x dopo un intervallo di tempo t.
Ovviamente la conoscenza esatta della trasformazione Tt è equivalente a saper risolvere le equazioni di Newton per tutte le condizioni iniziali, ma qui ci basta sapere che la trasformazione Tt è ben definita e poterne studiare le proprietà generali. Nel riquadro è descritto lo spazio delle fasi e la famiglia di trasformazioni Tt per un sistema particolarmente semplice, il pendolo.
|
Lo spazio delle fasi del pendolo
|
Un teorema importante, attribuito a Liouville, garantisce che le trasformazioni Tt conservano il volume dello spazio delle fasi [9]. La definizione del volume nello spazio delle fasi 2n-dimensionale è analoga alla definizione dell'area nel piano bidimensionale e del volume nello spazio tridimensionale: il volume del cubo Q costituito dagli stati (q1, q2, ..., qn, v1, v2, ..., vn) dove ciascuna delle variabili qj e vj varia in un intervallo di ampiezza L è L2n, mentre il volume di una regione qualsiasi si definisce approssimandola con tanti piccoli cubi. Il teorema di Liouville ci dice che se facciamo evolvere per un tempo t il cubo Q otteniamo una regione che non sarà più un cubo, ma che avrà ancora volume L2n.
Ma torniamo al problema di risolvere le equazioni di Newton. Per buona parte dell'Ottocento questo voleva dire determinare n integrali del moto, cioè n funzioni definite sullo spazio delle fasi che si mantengano costanti lungo l'evoluzione temporale. Immaginiamo che lo spazio delle fasi sia il mare e che i pesciolini che vi nuotano dentro descrivano l'evoluzione temporale degli stati. Un integrale del moto potrebbe in questo caso essere la temperatura: ciascun pesciolino ha la sua temperatura preferita e nuota solamente nell'acqua a quella temperatura. Che aspetto avrà la regione dove nuota il pesciolino che predilige i 6,7 gradi Celsius? Il mare è tridimensionale e la porzione a 6,7 gradi Celsius è una superficie in prima approssimazione orizzontale, ma che scende più in profondità nelle zone equatoriali e sempre meno avvicinandosi ai poli. Sapere che i pesciolini hanno una temperatura preferita non ci permette di prevederne il moto, ma almeno lo confina ad uno spazio di dimensione più bassa: una superficie bidimensionale, di una dimensione inferiore alle tre dello spazio delle fasi. Quindi l'effetto di ciascun integrale del moto è di ridurre di un'unità la dimensione della regione potenzialmente raggiungibile dall'evoluzione dei singoli stati. Se riusciamo a trovare n integrali del moto, tanti quanti sono i gradi di libertà, lo spazio delle fasi 2n-dimensionale viene suddiviso (matematicamente, foliato) in "superfici" di dimensione n, ciascuna delle quali è invariante per l'evoluzione. In effetti, la conoscenza di n integrali del moto permette anche di stabilire di che natura siano queste superfici e che aspetto qualitativo abbia il moto su di esse. Si veda il riquadro seguente per maggiori dettagli.
|
Sistemi completamente integrabili
Si dicono completamente integrabili quei sistemi con n gradi di libertà per cui è possibile trovare n integrali del moto. Indichiamo con i simboli ω1, ω2..., ωn questi n integrali del moto. Si dimostra che in questo caso un cambio di variabili nello spazio delle fasi permette di passare dalle coordinate (q1, q2, ..., qn, v1, v2, ..., vn) a coordinate ( φ1, φ2, ..., φn, ω1, ω2..., ωn) in cui il sistema mostra un comportamento molto semplice: le ωj sono costanti (già lo sapevamo, trattandosi di integrali del moto), mentre le φj sono coordinate angolari - nel senso che cambiando φj con φj+ 2π lo stato individuato non cambia - che compiono rotazioni complete con frequenza ωj, ossia φj (t) = φj (0) + ωjt. Fissiamo arbitrariamente i valori degli n integrali del moto. Che forma hanno le superfici dove è confinato il moto? Se n=1 abbiamo un solo angolo che varia, quindi il moto è confinato ad un cerchio. Se n=2 abbiamo due angoli che variano indipendentemente: la superficie descritta è quella di un toro, il termine matematico per indicare la superficie di una ciambella. In generale troviamo tori n-dimensionali. Come è il moto sul singolo toro? |
Qui ci basta osservare che con un opportuno cambio di variabili il sistema si comporta come n oscillatori indipendenti l'uno dall'altro, quindi esibisce un moto molto regolare. Alcuni integrali del moto sono evidenti, come l'energia, che si conserva in tutti i sistemi isolati dall'esterno, o la quantità di moto, o il momento angolare. Nell'Ottocento erano stati sviluppati vari metodi per trovare gli integrali del moto meno evidenti, per arrivare ai fatidici n che permettono una comprensione pressoché completa della dinamica. Questi metodi avevano permesso di studiare con successo due corpi che si attraggono tramite la forza gravitazionale, pendoli multipli, trottole ed altri sistemi relativamente semplici. Applicare gli stessi metodi a sistemi più complicati sembrava un'impresa difficile dal punto di vista algebrico, ma non impossibile. Tra i problemi più importanti che sembravano resistere ad ogni attacco, la descrizione del moto di tre o più corpi che si attraggono tramite la forza gravitazionale meritò di essere inclusa in un concorso internazionale di matematica, bandito da Re Oscar II di Svezia nel 1886. Ecco come il matematico Weierstrass enunciò il problema nel bando di concorso:
Dato un sistema composto da un numero qualsiasi di punti materiali che si attirano mutuamente secondo la legge di Newton, si propone, nell'ipotesi che fra due punti non si verifichino mai urti, di rappresentare le coordinate di ciascun punto sotto forma di serie di potenze di funzioni continue nel tempo che siano uniformemente convergenti per tutti i valori reali della variabile.
Vinse il concorso il matematico francese Henri Poincaré, con una memoria in cui, tra vari altri risultati, forniva una risposta di tipo negativo al problema formulato da Weierstrass: se i corpi sono più di due, non esistono altri integrali del moto oltre a quelli già conosciuti. Più tardi dimostrerà che "genericamente" le equazioni di Newton non hanno integrali del moto diversi dall'energia. Dunque il metodo della ricerca degli integrali del moto non aveva la validità generale che gli si attribuiva e il comportamento di un sistema meccanico appariva improvvisamente molto più complesso di quanto si ritenesse. La frase di Laplace citata sopra rimaneva vera alla lettera, ma le capacità dell' "intelletto incaricato di sottoporre i dati ad analisi" dovevano essere ben superiori di quanto immaginasse Laplace [10].
Le idee di Boltzmann
Abbiamo ormai tutti gli strumenti per poter seguire il ragionamento con cui Boltzmann spiegò la nascita dell'irreversibilità a partire da equazioni reversibili. La soluzione di acqua e inchiostro è un sistema troppo complicato, quindi consideriamone uno più semplice: un gas monoatomico dentro un contenitore diviso in due parti uguali da una parete mobile. All'inizio il gas occupa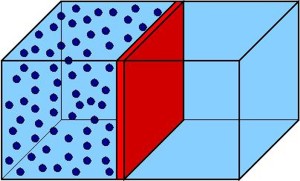
soltanto una metà del contenitore, poiché la parete gli impedisce l'accesso all'altra metà, poi la parete viene rimossa e il gas diventa libero di espandersi. Questo sistema mostra un chiaro comportamento irreversibile: una volta rimossa la parete il gas si espande in tutto il contenitore, fino a raggiungere una densità uniforme. Non ci aspettiamo di vederlo tornare spontaneamente nella metà di partenza. Possiamo pensare agli atomi che compongono il gas come a particelle puntiformi tra le quali agisce una forza repulsiva che si attiva quando due particelle si avvicinano (o una si avvicina alle pareti del contenitore) oltre una certa soglia. Se il gas è composto da N atomi, questo sistema ha 3N gradi di libertà, dunque lo spazio delle fasi ha dimensione 6N. 
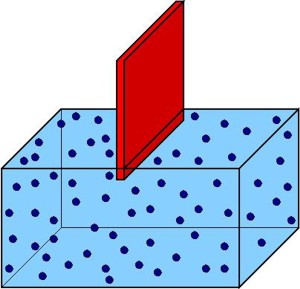Il sistema è isolato, quindi l'energia totale si conserva: questo integrale del moto confina la dinamica ad uno spazio di dimensione 6N-1.
I risultati di Poincaré ci fanno sospettare che non vi siano altri integrali del moto, quindi ciascuno stato potenzialmente è libero di muoversi per tutto lo spazio di dimensione 6N-1 corrispondente al valore dell'energia totale. Chiamiamo X questo spazio.
A questo punto Boltzmann formula la sua famosa ipotesi ergodica: l'evoluzione di un generico stato invade tutto [11] lo spazio X trascorrendo pari frazioni di tempo in regioni di pari volume. Qua generico sta a significare che chiediamo che questa proprietà valga per tutti gli stati tranne che per eventuali stati eccezionali, che si richiede formino un insieme di volume nullo. Anche se molto difficile da dimostrare [12], si tratta di un'ipotesi ragionevole. A favore dell'ipotesi che l'evoluzione di un generico stato tenda ad invadere tutto X gioca l'alta sensibilità del moto alle condizioni iniziali (il fatto che piccole differenze nelle condizioni iniziali causano grandi differenze nell'evoluzione futura), a sua volta conseguenza delle miriadi di collisioni tra gli atomi. La proporzionalità tra il tempo trascorso in una regione ed il suo volume è suggerita dal fatto che, come abbiamo osservato, la dinamica su X conserva il volume [13]. Parecchi anni più tardi Birkhoff dimostrerà che l'ipotesi ergodica è equivalente a chiedere che non sia possibile suddividere lo spazio X in due regioni di volume positivo invarianti per la dinamica. I sistemi con questa proprietà si dicono ergodici [14]. Tornando all'esempio del mare come spazio delle fasi, è ergodico quel sistema dove i pesciolini nuotano liberamente per tutto il mare, senza creare zone dove sono confinati solo alcuni dei pesciolini.
Qual è il volume di X e quale il volume della regione A costituita da quegli stati che corrispondono alla situazione in cui tutto il gas occupa una metà - diciamo quella sinistra - del contenitore? Per poter portare a termine questo calcolo, reso complicato dalla geometria di X, operiamo una semplificazione un po' rozza, ma che non snatura gli aspetti salienti di quello che sarebbe l'approccio corretto: supponiamo che la conservazione dell'energia totale abbia il solo effetto di costringere ciascuna particella ad avere una velocità non superiore ad una certa velocità massima, che indichiamo con M. Grazie a questa semplificazione lo spazio X ha ancora dimensione 6N ed è costituito dagli stati (q1, q2, ..., qN, v1, v2, ..., vN) dove i qj sono vettori posizione che variano nel contenitore, mentre i vettori velocità vj hanno lunghezza al più M e direzione qualsiasi, dunque variano in una sfera di raggio M. Il contributo al volume di X di ciascun qj è pari al volume del contenitore, che indichiamo con V, mentre quello di ciascun vj è pari al volume della sfera di raggio M, ossia 4/3 π M3. Moltiplicando tra loro tutti questi contributi troviamo che il volume di X è
vol ( X ) = VN (4/3 π M3)N.
Il calcolo del volume di A, la regione di X che corrisponde al gas nella metà sinistra del contenitore, è analogo: l'unica differenza è che adesso il contributo di ciascun qj è pari a metà del volume del contenitore. Otteniamo quindi
vol ( A ) = (V/2)N(4/3 π M3)N.
La quantità significativa è il rapporto tra questi due volumi:
vol ( A ) / vol ( X ) = 1/2N,
ovvero il volume di A è 2N volte inferiore al volume di X. Dato che il numero N degli atomi di gas in un contenitore è tipicamente dell'ordine di 1023, 2N è un numero spaventosamente grande, un 1 seguito da qualcosa come 3・1022 zeri. L'ipotesi ergodica garantisce che la frazione di tempo che lo stato del sistema trascorre dentro A è 1/2N, un numero incredibilmente piccolo. Anche senza essere risolte esplicitamente, le equazioni di Newton ci dicono che dopo che il gas ha abbandonato la metà sinistra del recipiente sarà molto improbabile ritrovarvelo, nel senso che il tempo che dobbiamo aspettare affinché ciò accada è di parecchi ordini di grandezza più grande dell'età dell'universo.
La conclusione di Boltzmann è che un comportamento irreversibile non è una conseguenza inevitabile delle equazioni della meccanica, ma ne è una conseguenza altamente probabile, e per sistemi con molti gradi di libertà questa probabilità è talmente grande da diventare, a tutti gli effetti pratici, una certezza.
Boltzmann ha anche mostrato come l'irreversibilità si possa misurare quantitativamente, introducendo il suo concetto di entropia. Si veda il riquadro seguente per ulteriori dettagli.
|
L'entropia di Boltzmann Scegliamo una misurazione macroscopica F da effettuare sul nostro gas di N particelle, ad esempio la densità media del gas nella metà destra del contenitore. Dato che il volume di metà recipiente è V/2, se nella metà destra vi sono m particelle F vale 2m/V. La misurazione F definisce una funzione sullo spazio X degli stati di energia fissata, che assume valori nell'intervallo di estremi 0 e 2N/V. Dividiamo questo intervallo in 5 parti uguali, ed usiamo i valori assunti da F per suddividere X in 5 regioni X1, X2, X3, X4, X5: X1 è l'insieme di quegli stati dove nella metà destra vi sono meno di N/5 particelle, X2 è l'insieme dove ve ne sono da N/5 a 2N/5, e così via. Qui stiamo semplificando l'argomento: in effetti dovremmo suddividere X in un numero molto più grande di regioni, ma piccolo rispetto ad N. L'entropia di Boltzmann di uno stato x appartenente alla regione Xj è definita come il logaritmo del volume di Xj: SB(x) = log vol (Xj).
Usando la definizione semplificata di X introdotta in precedenza, il lettore è invitato a calcolare il volume della regione Xj e a verificare che il rapporto vol (Xj) / vol (X) è pari alla somma dei coefficienti binomiali |
per h compreso tra (j-1)N/5 e jN/5, diviso per 2N. Ricordando che i coefficienti binomiali
Cosa ci impedisce di invertire la freccia del tempo con una scelta di condizioni iniziali opportune? Supponiamo di disporre di un apparecchio fantascientifico che ci permetta di far partire ciascun atomo del gas dalla posizione e con la velocità desiderata, con un margine di errore piccolissimo. Partiamo come prima da uno stato appartenente ad A, l'insieme degli stati che descrivono il gas concentrato in metà recipiente. Trascorso un certo periodo di tempo, diciamo dieci secondi, lo stato del sistema è passato dalla regione iniziale A ad una certa regione B, che si ottiene facendo evolvere per dieci secondi tutti gli stati di A, e che sappiamo avere lo stesso volume. Se riuscissimo a portare lo stato del sistema nella regione C, ottenuta a partire dagli stati della regione B invertendo tutte le velocità, vedremmo un gas che si concentra e in dieci secondi va ad occupare metà del contenitore: avremmo così invertito la freccia del tempo. La regione C ha ancora lo stesso volume di B, quindi lo stesso volume di A. Eppure mentre portare lo stato nella regione A è semplice (basta usare un pistone), neanche l'uso del nostro apparecchio fantascientifico ci consente di portare lo stato nella regione C. Perché?
Il motivo sta nella già menzionata alta sensibilità alle condizioni iniziali. La regione A ha un aspetto piuttosto regolare: ha volume piccolissimo e occupa una porzione piccolissima dello spazio delle fasi. Dopo dieci secondi di evoluzione gli stati di A sono andati ad invadere tutto lo spazio delle fasi, pur conservando il piccolo volume che aveva A. Ciò vuol dire che l'insieme B così ottenuto risulta molto irregolare, quasi rarefatto. Una buona analogia è pensare ad A come ad una goccia di inchiostro appena caduta in un bicchiere d'acqua e a B come la sua evoluzione dopo alcuni istanti, quando l'inchiostro ha ormai colorato tutta l'acqua: l'inchiostro si trova ovunque, ma se prendiamo una molecola a caso dal bicchiere quasi sicuramente sarà una molecola d'acqua.
L'insieme C è ottenuto a partire da B tramite una semplice riflessione (vengono invertite le velocità) quindi continua ad avere la stessa geometria. Se impostiamo il nostro apparecchio fantascientifico su un determinato stato, a causa dei pur minimi errori verrà prodotto uno stato vicino. Impostandolo su uno stato all'interno della regione A, lo stato vicino prodotto starà ancora in A. Invece, impostandolo su uno stato di C, lo stato prodotto starà quasi certamente fuori da C e non evolverà verso A.
Gli ingredienti dell'irreversibilità
Abbiamo visto che gli ingredienti dell'irreversibilità sono una certa eccezionalità delle condizioni iniziali, un gran numero di gradi di libertà, ed una sufficiente ergodicità. In che misura questi diversi ingredienti concorrono alla formazione della freccia del tempo?
L'eccezionalità delle condizioni iniziali è essenziale. Nell'evoluzione di gas, liquidi ed altri sistemi complessi l'irreversibilità si manifesta se possiamo partire da condizioni iniziali eccezionali, lontane dall'equilibrio e corrispondenti a regioni di volume piccolissimo nello spazio delle fasi, in altre parole se possiamo partire da stati iniziali di bassa entropia.
Condizioni iniziali eccezionali permettono la formazione della freccia del tempo anche in assenza degli altri due ingredienti: pensiamo ad una palla che rotola su un piano orizzontale posto a tre metri di altezza e che alla fine del piano cade giù in mano ad un ragazzo. Se filmiamo questa scena e la rivediamo in reverse vedremo un ragazzo che lancia una palla su di un piano posto al di sopra della sua testa, con tanta precisione che quella arriva con velocità verticale nulla ed inizia a rotolare senza fare alcun rimbalzo. Chi vedesse il video in reverse sospetterebbe subito la manipolazione, quindi in questo sistema fa la comparsa una pur debole freccia del tempo, dovuta al fatto che le condizioni iniziali in cui la palla ha componente verticale della velocità nulla formano un insieme di volume trascurabile nello spazio delle fasi di questo sistema. Però il fatto che qui la dinamica non sia fortemente sensibile alle condizioni iniziali rende possibile, seppure difficile, il compito di un ragazzo che volesse realizzare dal vivo il lancio che si vede nel video in reverse.
Ma come è possibile creare condizioni iniziali eccezionali, o con bassa entropia, come quella di un gas che occupa metà di un recipiente? Basta che uno sperimentatore spinga un pistone, aumentando leggermente la propria entropia, che provvederà a riabbassare facendo uno spuntino, ossia consumando alimenti a bassa entropia. Alimenti che traggono la loro bassa entropia dal sole, anch'esso in una situazione di bassa entropia. Di questo passo si è naturalmente condotti a considerazioni di natura cosmologica e all'ipotesi che lo stato iniziale dell'universo fosse uno stato di bassa entropia. Ne era ben conscio Boltzmann, che considerava questa come un'ipotesi inevitabile e non deducibile da principi più fondamentali. Cosmologi moderni, come Roger Penrose, nutrono la speranza di poter dedurre la bassa entropia dell'universo del big bang da principi più basilari.
Abbiamo usato l'ipotesi ergodica per giustificare il fatto che il volume di una regione dello spazio delle fasi sia proporzionale alla probabilità che la traiettoria di un generico stato si trovi ad un dato istante in tale regione. Eppure i sistemi con un gran numero di gradi di libertà mostrano comportamenti irreversibili anche senza esibire una vera ergodicità, nel senso matematico del termine. Un gas i cui atomi non interagiscono tra loro costituisce un sistema che ergodico non è, dato che la velocità di ciascun atomo è un integrale del moto, eppure non lo vedremo tornare ad occupare la metà recipiente da cui era partito [15]. Il motivo è che questo sistema è in un certo senso ergodico rispetto alla misurazione che stiamo facendo, quella di contare il numero delle particelle contenute in metà recipiente. Facendo altri tipi di esperimenti con questo gas non vedremmo comparire alcuna freccia del tempo. Mescoliamo due quantità di gas, la prima composta da atomi le cui velocità sono distribuite vicino ad un certo valore medio va, la seconda in cui la distribuzione delle velocità è vicina ad un valore medio vb, diverso da va. Se gli atomi non interagiscono, le velocità si conservano e sarà possibile in futuro separare nuovamente le due quantità di gas. Qua l'irreversibilità non appare. Se invece gli atomi interagiscono, le loro velocità tenderanno ad assumere una distribuzione Gaussiana - la curva dalla classica forma a campana - attorno ad un valore intermedio tra va e vb (un altro risultato descritto quantitativamente da Boltzmann). Separare gli atomi dei due gas diventa quindi impossibile: in un gas di atomi interagenti l'irreversibilità si manifesta anche in questo esperimento.
Osservando un gas, un liquido o altri sistemi complessi, le misurazioni macroscopiche che possiamo fare sono relativamente poche rispetto al grande numero di gradi di libertà. A ciascuna di queste misurazioni corrisponde una funzione sullo spazio delle fasi, che assume valori vicini ad un comune valore di equilibrio su gran parte dello spazio delle fasi, e presenta notevoli differenze soltanto in una regione eccezionale di volume piccolissimo. Il rapporto tra il volume della regione eccezionale e il volume di tutto lo spazio è esponenzialmente piccolo rispetto al numero dei gradi di libertà. Solo alle zone eccezionali si deve applicare l'ipotesi ergodica; se anche questa non fosse valida in senso stretto, ma le zone eccezionali venissero visitate cento, mille, un milione di volte più spesso di quanto previsto dall'ergodicità, il loro volume è talmente piccolo che la probabilità che una volta raggiunto il valore di equilibrio il sistema possa discostarsene è trascurabile.
Per sistemi con pochi gradi di libertà comportamenti irreversibili, in ogni caso quantitativamente diversi da quelli di sistemi con molti gradi di libertà, possono apparire solamente in presenza di buone proprietà ergodiche. Immaginiamo di vedere in un video 15 palle numerate ed una bianca rimbalzare tra loro e sulle sponde di un tavolo da biliardo. Ad un certo punto le palle numerate si riuniscono a formare un triangolo da cui viene sparata fuori la palla bianca. Anche chi non ha mai visto una spaccata nel biliardo all'americana intuirà che sta vedendo un video in reverse. Qui i gradi di libertà, trascurando le rotazioni delle palle attorno ai loro assi, sono solamente 32, ma grazie all'ergodicità e alla scelta di una condizione iniziale particolarissima sono sufficienti alla formazione della freccia del tempo.
Le reazioni a Boltzmann
Le idee di Boltzmann incontrarono una generale ostilità presso i contemporanei. Particolarmente critici furono Loschmidt, Mach, Zermelo, e vi furono incomprensioni anche da parte di chi, come i coniugi Erhenfest, sostennero e svilupparono le idee di Boltzmann.
Zermelo in particolare criticò l'approccio di Boltzmann in base al teorema di ricorrenza di Poincaré. Si tratta di un teorema molto generale, che afferma che se lo spazio X ha volume finito e la dinamica su X conserva il volume, allora un generico stato di una qualunque regione A ritorna in A per tempi arbitrariamente grandi (come prima, “generico” significa che ciò accade a tutti gli stati di A, tranne che eventualmente a stati appartenenti ad una regione di volume nullo). Secondo Zermelo questo fatto esclude la possibilità di dedurre un comportamento irreversibile da un modello meccanico come quello studiato da Boltzmann. Boltzmann non ebbe difficoltà a rispondere a questa critica, mostrando che nei sistemi da lui considerati il tempo di ricorrenza previsto dal teorema di Poincaré è astronomicamente grande. In effetti il tempo di ricorrenza per la regione A è inversamente proporzionale al volume di A e cresce all'aumentare delle proprietà ergodiche del sistema. Perciò un gran numero di gradi di libertà - responsabile della piccolezza dei volumi delle regioni dove il sistema è lontano dall'equilibrio - e/o una buona ergodicità annullano per scale di tempo fisicamente ragionevoli gli effetti della ricorrenza.
Altre critiche ed incomprensioni derivarono invece da ciò che è oggi riconosciuto come un altro dei grandi meriti dello scienziato austriaco: l'uso della probabilità nello studio dei sistemi deterministici. Il comportamento irreversibile del gas nel recipiente diviso in due parti può essere spiegato in maniera molto semplice ricorrendo a modelli probabilistici, come quello che gli Erhenfest proposero per illustrare le idee di Boltzmann: si immagina che gli N atomi siano numerati, che ad ogni istante venga estratto a sorte un numero da 1 a N e che l'atomo corrispondente venga spostato dalla metà del recipiente in cui si trova nell'altra. Se all'inizio gli atomi sono tutti a sinistra, la prima estrazione comporterà lo spostamento di uno degli atomi a destra. Al secondo istante sarà molto improbabile che venga estratto lo stesso numero, quindi sarà molto probabile che un secondo atomo da sinistra si sposti a destra. Finché a destra non vi è un numero di atomi paragonabile a quello degli atomi presenti a sinistra, sarà molto probabile che l'atomo sorteggiato stia da quest'ultima parte e si osserverà un flusso di atomi da sinistra a destra. Una volta raggiunto l'equilibrio gli spostamenti da sinistra a destra e da destra a sinistra saranno ugualmente probabili e l'equilibrio si manterrà. Questo modello descrive abbastanza bene il comportamento di un gas, però a prima vista appare molto lontano dalle equazioni deterministiche che sappiamo regolare il moto degli atomi. Eppure le idee di Boltzmann permettono di dimostrare che un sistema che obbedisce a queste equazioni esibisce un comportamento analogo a quello del modello probabilistico degli Erhenfest.
Naturalmente altri contemporanei condividevano le idee di Boltzmann sul ruolo della probabilità nelle scienze esatte. Non saprei trovare parole migliori di quelle di Poincaré per descrivere questo ruolo:
Una causa minima, che ci sfugge, determina un effetto considerevole, del quale non possiamo non accorgerci: diciamo allora che questo effetto è dovuto al caso. Se conoscessimo con esattezza le leggi della natura e lo stato dell'universo all'istante iniziale, potremmo prevedere quale sarà lo stato di questo stesso universo ad un istante successivo. Ma quand'anche le leggi naturali non avessero per noi più segreti potremo conoscere lo stato iniziale soltanto approssimativamente. Se ciò ci permette di conoscere lo stato successivo con la stessa approssimazione, non abbiamo bisogno d'altro, e diremo che il fenomeno è stato previsto, che esistono leggi che lo governano. Ma non sempre è così: può succedere che piccole differenze nelle condizioni iniziali generino differenze grandissime nei fenomeni finali; un piccolo errore a proposito delle prime genererebbe allora un errore enorme a proposito di questi ultimi. La previsione diventa impossibile: siamo di fronte al fenomeno fortuito.
E soprattutto:
Mi chiedete di prevedere i fenomeni che stanno per verificarsi. Se per disgrazia conoscessi le leggi di questi fenomeni, non sarei in grado di farlo se non a prezzo di calcoli inestricabili e dovrei rinunciare a rispondervi; ma siccome ho la fortuna di ignorarle, vi risponderò immediatamente. E quel che vi è di più straordinario in tutto ciò è che la mia risposta sarà corretta [16].
Critiche a Boltzmann e ricerche di soluzioni alternative sono proseguite anche in anni più recenti. Tra i critici più noti, i filosofi Bergson, Popper, Feyerabend e il premio Nobel per la chimica Prigogine (l'articolo [A] contiene un'analisi rigorosa di queste critiche ed una difesa delle idee di Boltzmann, il libro [D] esprime una posizione opposta).
Stabilità inaspettate
Per conto nostro ci dichiariamo più che soddisfatti dalla spiegazione di Boltzmann. Ma se l'origine dei comportamenti irreversibili ci è chiara, cosa dire di quei sistemi dove l'irreversibilità non si presenta? Al pendolo a forma di cavaliere certamente mancano i requisiti fondamentali: si tratta di un sistema completamente integrabile con pochi gradi di libertà. Però come mai sistemi complessi come i sistemi planetari o le galassie seguono moti che ci appaiono reversibili?
Il nostro sistema solare contiene una miriade di asteroidi, concentrati essenzialmente tra le orbite di Marte e di Giove. Perché le interazioni tra loro e quelle con i pianeti non fanno sì che gli asteroidi si distribuiscano per tutto il sistema solare?
Un altro esempio nasce da una delle prime simulazioni al computer, quella che Fermi, Pasta e Ulam realizzarono nell'estate del 1953 con il MANIAC, uno dei primi computer mai costruiti. I tre scienziati simularono l'evoluzione di un sistema costituito da un gran numero di oscillatori armonici, accoppiati da deboli forze non lineari. Gli accoppiamenti, ancorché deboli, distruggono la completa integrabilità del sistema disaccoppiato e visto il gran numero di gradi di libertà ci si aspettava di assistere ad una rapida equipartizione dell'energia: eccitando inizialmente solo alcuni dei pendoli, la loro energia doveva trasmettersi agli altri in modo da raggiungere presto un equilibrio in cui tutti gli oscillatori hanno pressappoco la stessa energia. Invece nella simulazione di Fermi, Pasta e Ulam questa convergenza all'equilibrio non sembrava manifestarsi.
Nel 1954 il matematico russo Kolmogorov scoprì un nuovo aspetto dei sistemi meccanici che poteva spiegare questi fenomeni. I suoi risultati furono migliorati da Arnold e Moser nel decennio successivo, andando a formare quella che adesso si chiama teoria KAM, dalle iniziali dei tre matematici.
La teoria KAM riguarda sistemi che possono essere visti come piccole perturbazioni di sistemi completamente integrabili: sono di questo tipo tanto il sistema studiato da Fermi, Pasta e Ulam quanto i sistemi planetari, dato che la grande differenza fra le masse in gioco fa sì che le interazioni tra i corpi in orbita siano di gran lunga più deboli delle loro interazioni con la stella centrale, e dato che il sistema in cui si considerano solo queste ultime è completamente integrabile.
Il secondo riquadro ("Sistemi completamente integrabili") mostra come lo spazio delle fasi di un sistema completamente integrabile sia foliato da tori invarianti per la dinamica. Su ciascun toro la dinamica è data da moti quasi- periodici, ottenuti cioè combinando n rotazioni indipendenti, con frequenze ω1, ω2..., ωn date dal valore degli integrali del moto su quel toro.
La teoria KAM dimostra che nel sistema perturbato i tori invarianti corrispondenti a frequenze in rapporto molto irrazionale sopravvivono, magari un po' modificati, mentre gli altri tori vengono distrutti. Vediamo cosa si intenda per "frequenze in rapporto molto irrazionale", limitandoci per semplicità al caso n=2. In questo caso le frequenze sono soltanto due e stiamo chiedendo che il loro rapporto ω1/ω2 sia un numero irrazionale che si approssima male con numeri razionali. Tecnicamente, chiediamo che ω1/ω2 sia un numero Diofanteo.
|
I numeri diofantei Ogni numero irrazionale α è approssimabile con la precisione desiderata da un numero razionale, ma al costo di scegliere il denominatore di quest'ultimo sufficientemente grande. Ad esempio se q è un intero positivo, possiamo approssimare α a meno di 1/q con un razionale che ha per denominatore proprio q, come il lettore potrà facilmente verificare. Più impegnativo è dimostrare il risultato seguente, dovuto a Liouville: per ogni numero reale α esiste una successione di interi positivi qh che cresce indefinitamente ed esistono interi ph tali che | α - ph/qh| ≤ 1/qh2. Dire che α è Diofanteo significa che questo ordine di approssimazione non è migliorabile di molto. Più precisamente, α è Diofanteo se esistono numeri β > 2 e γ > 0 tali che | α - p/q | ≥ γ/qβ per ogni scelta del numero razionale p/q. Scoprendo un inaspettato collegamento tra la teoria dei numeri e la meccanica, la teoria KAM dimostra che nei sistemi con due gradi di libertà sono i tori con rapporto tra le frequenze Diofanteo a sopravvivere alle piccole perturbazioni. |
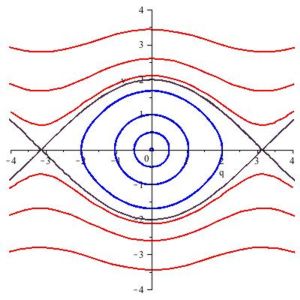
Dunque in un sistema vicino ad uno completamente integrabile una gran parte dei tori invarianti e dei relativi moti quasi-periodici sopravvive, mentre altri vengono distrutti, lasciando alcuni stati liberi di seguire moti molto complicati. La figura seguente mostra una sezione dello spazio delle fasi di un sistema di questo tipo: in blu sono rappresentati gli stati che appartengono a tori sopravvissuti, in rosso gli altri stati.
Quanto più piccola è la perturbazione del sistema completamente integrabile, tanto maggiore è il volume occupato da quei tori che sopravvivono. Sistemi di questo tipo, per quanto non abbiano in generale integrali del moto diversi dall'energia, sono molto lontani dall'ergodicità: gli stati che appartengono ad uno dei molti tori che sopravvivono vi rimarranno confinati per sempre, dando origine a moti quasi-periodici e senza far nascere alcuna freccia del tempo.
Misurare posizione e velocità
Concludiamo questo nostro excursus nella meccanica parlando di un teorema importante, anche se non direttamente collegato al problema dell'irreversibilità.
Consideriamo un sistema meccanico con n ≥ 2 gradi di libertà. Supponiamo di conoscere lo stato del sistema a meno di una precisione R in tutte le coppie di variabili posizione-velocità. Questo significa che se valutiamo che lo stato del sistema sia (Q1, Q2, ..., Qn, V1, V2, ..., Vn), lo stato vero è un certo (q1, q2, ..., qn, v1, v2, ..., vn) dove
(qj - Qj)2+ (vj - Vj)2≤ R2, (1)
per ogni j da 1 a n. Vorremmo far evolvere lo stato del sistema in modo da migliorare contemporaneamente la nostra conoscenza di una coppia di variabili posizione-velocità, per fissare le idee la q1 e la v1. Per esempio potremmo voler conoscere meglio la componente verticale della posizione e della velocità di una determinata particella. Per realizzare ciò occorre che l'evoluzione temporale del sistema porti la regione definita dalle n disuguaglianze (1) nella regione costituita dagli stati (q1, q2, ..., qn, v1, v2, ..., vn) che verificano la sola disuguaglianza
(q1 - Q )2+ (v1 - V )2≤ S2, (2)
dove il numero S è inferiore ad R ed è il nuovo livello di precisione desiderato (qua Q e V sono le nuove stime per q1 e v1). Il teorema di Liouville non ci impedisce di realizzare una evoluzione di questo tipo. Infatti la regione definita dalle equazioni (1) ha volume finito [17], mentre quella definita dalla (2) ha volume infinito, dato che tutte le variabili qj e vj con j ≥ 2 sono libere (questa regione deve essere pensata come un cilindro infinito avente per base il cerchio di raggio S nelle variabili q1 e v1). È certamente possibile mandare una regione di volume finito dentro una di volume finito tramite una trasformazione che conservi il volume.
Eppure nel 1985 il matematico russo Mikhail Gromov ha dimostrato che se S < R nessuna trasformazione della meccanica [18] può mandare la regione definita dalle equazioni (1) dentro quella definita dalla (2). Si noti che sarebbe invece molto semplice migliorare la conoscenza di tutte le posizioni q1, q2, ..., qn a scapito di tutte le velocità v1, v2, ..., vn, come pure il viceversa.
Parte del fascino di questo teorema è dovuta ad una suggestiva analogia con uno dei principi fondamentali della meccanica quantistica, il principio di indeterminazione di Heisenberg. Esso afferma che, mentre è possibile misurare la posizione oppure la velocità di una particella con precisione arbitraria, non è possibile misurarle entrambe con una precisione congiunta che superi una certa soglia. Per quanto imperfetta (nella meccanica classica non appare una soglia privilegiata), l'analogia con il teorema di Gromov è evidente.
Nel teorema di Gromov si parte da una precisione uniforme, data dal numero R, su tutte le variabili. Se invece la precisione iniziale non è uniforme si aprono nuove possibilità, come ha mostrato nel 2006 il matematico americano Larry Guth costruendo una trasformazione meccanica dalle proprietà inaspettate. In un sistema con tre particelle conosciamo la posizione e la velocità della prima con ottima precisione, data da un numero arbitrariamente piccolo ε, mentre conosciamo la posizione e la velocità delle altre due particelle con precisione media, diciamo di ordine 1. La trasformazione di Guth permette di guadagnare un'ottima precisione sulla conoscenza di posizione e velocità della seconda particella, senza per questo perdere significativamente quella sulla prima e al solo scapito di quella sulla terza. Più quantitativamente, alla fine della trasformazione la posizione e la velocità della prima particella risultano note con precisione 2ε, quelle della seconda con precisione 10ε, mentre quelle della terza sono essenzialmente ignote. Ricorrendo ad un'analogia chimica, possiamo dire che la prima particella si comporta come un catalizzatore, mentre la terza è un prodotto di scarto.
Né il teorema di Gromov né la costruzione di Guth hanno ancora trovato significative applicazioni fisiche, ma mostrano quanta ricchezza si celi nelle equazioni della meccanica. Equazioni che matematici e fisici guardano da oltre tre secoli. In questi tre secoli molti altri principi e molte altre equazioni sono stati introdotti per spiegare i fenomeni che accadono alle scale subatomiche o astronomiche. Eppure le equazioni scritte da Newton conservano la loro validità nella descrizione di una vastissima gamma di fenomeni. Per questo matematici e fisici continuano a studiarle e generazione dopo generazione vi scoprono qualcosa di nuovo.
Le equazioni sono sempre le stesse, ma la loro struttura è talmente ricca che le idee sulle loro implicazioni, per non parlare delle tecniche nell'affrontarle, sono mutate profondamente. Newton, Laplace, Liouville, Poincaré, Boltzmann, Kolmogorov, Arnold, Moser e Gromov sono soltanto alcuni dei protagonisti di un avvenura intellettuale che promette di proseguire ancora per molti anni.
Ringraziamenti
Si ringrazia Arrigo Amaduzzi per i materiali e per la consulenza nella realizzazione dei video.
Bibliografia
[A] J. Bricmont, Science in chaos or chaos in science?, in "The flight from science and reason", Annals of the New York Academy of Science 79 (1996), pag. 131. Reperibile all'indirizzo web http://arxiv.org/abs/chao-dyn/9603009.
[B] G. Gallavotti, Meccanica statistica, voce per la Enciclopedia delle scienze fisiche edita dalla Enciclopedia Italiana, vol. III pag. 723-740, 1993.
[C] J. Lebowitz, Boltzmann entropy and time's arrow, Physics Today (1993), pag. 32-38. Reperibile all'indirizzo web http://www.math.rutgers.edu/~lebowitz/PUBLIST/lebowitz_370.pdf.
[D] I. Prigogine, La fine delle certezze, Bollati Boringhieri 1997.
[E] D. Ruelle, Caso e caos, Bollati Boringhieri 1992.
[1] Martin Amis, The time arrow, Penguin 1991 (trad. it. La freccia del tempo, Mondadori, 1993). “Anche mangiare perde ogni attrattiva [...] Scelgo un piatto sporco, vi sistemo degli avanzi di cibo presi dalla pattumiera e mi metto comodo per un po'. Alcuni bocconi vengono rigurgitati nella mia bocca e, dopo un abile massaggio con la lingua e con i denti, li trasferisco sul piatto per un'ulteriore lavorazione con coltello, forchetta e cucchiaio. È quasi terapeutico, a meno che non si abbia a che fare con una zuppa o qualcosa del genere, nel qual caso è una vera tortura. Poi affronto la laboriosa faccenda del raffreddamento, del riassemblaggio, dell'immagazzinaggio, prima di riportare gli alimenti al supermercato dove, devo riconoscerlo, vengo prontamente e generosamente rimborsato per le mie sofferenze. Poi con il carrello o il cestello percorro a ritroso le corsie, rimettendo tutta la mercanzia al proprio posto.” (TdR)
[2] L'accelerazione e la forza sono grandezze vettoriali, in quanto servono tre componenti spaziali per determinarle. Adottiamo la convenzione di indicare in grassetto le grandezze vettoriali.
[3] Il lettore che abbia dimestichezza con il moto circolare può provare ad eseguire lo stesso esperimento mentale con un treno che si muova in curva con velocità costante.
[4] Vi sono anche forze, come quelle magnetiche, che dipendono dalla velocità del corpo su cui agiscono. In presenza di tali forze la reversibilità dell'equazione di Newton è da intendersi in un senso diverso da quello che discutiamo qui.
[5] Questo è il contenuto del Teorema di Picard-Lindelöf o di Cauchy-Lipschitz, dal nome dei matematici a cui è associata la dimostrazione studiata ancora oggi nei corsi universitari.
[6] Qui parliamo di sistemi della fisica classica, siste mi cioè dove le velocità non siano prossime a quelle della luce (che richiedono una trattazione relativistica) e dove non siano rilevanti le singole interazioni tra particelle elementari (per le quali è necessaria la meccanica quantistica). Pressoché tutti i fenomeni che avvengono a scala umana rientrano nell'ambito della fisica classica.
[7] Pierre Simon de Laplace, Essai philosophique sur les probabilités, 1825 (trad. it. S. Oliva, Laterza 1951).
[8] L'uso di un computer ci permette di calcolare soluzioni approssimate, ma in generale la qualità dell'approssimazione peggiora al crescere del tempo e per tempi grandi tali soluzioni approssimate sono inservibili.
[9] Questa proprietà è dovuta alla natura Hamiltoniana delle equazioni di Newton, cioè al fatto che le componenti delle forze sono - a meno del segno - le derivate parziali di una funzione V(q1,q2,...,qn), detta energia potenziale.
[10] Ed è bene sottolineare come il paradigma determinista di Laplace resti valido ancora oggi, almeno per la maggior parte degli scienziati. L'introduzione della meccanica quantistica ci obbliga ad interpretare diversamente questo paradigma, ma come abbiamo già osservato la descrizione di tutti i fenomeni a scala umana generalmente non richiede la meccanica quantistica.
[11] Qua "tutto" non va inteso in senso letterale: la traiettoria di uno stato è una curva regolare, ossia qualcosa di dimensione uno che non può riempire uno spazio di dimensione più alta. Quello che intendiamo è che qualunque regione di volume positivo prima o poi viene visitata dalla traiettoria.
[12] Non sono molti i sistemi di cui si sappia dimostrare rigorosamente l'ergodicità. Grazie ad un lavoro di Sinai del 1963, appartiene a questa classe il moto di una pallina in un tavolo da biliardo con ostacoli convessi, un sistema che presenta buone analogie con i gas.
[13] In effetti introducendo il Teorema di Liouville abbiamo parlato di volume dello spazio delle fasi, non di volume nello spazio X, che ha una dimensione in meno ed è in generale uno spazio curvo. Il fatto che sullo spazio X sia possibile definire un volume conservato dalla dinamica è una conseguenza del Teorema di Liouville. È questo il volume a cui ci stiamo riferendo.
[14] Per l'etimologia della parola ergodico si veda [B].
[15] Però in questo caso l'apparecchio fantascientifico del capitolo precedente ci permetterebbe di invertire la freccia del tempo.
[16] Henri Poincaré, Le hasard, Revue du mois, 1907. Riprodotto in traduzione italiana nella raccolta di scritti di Poincaré Geometria e Caso, Bollati Boringhieri 1995.
[17] La coppia di variabili (qj,vj) varia in un cerchio di raggio R, che ha area π R2. Il volume della regione individuata dalle disuguaglianze (1) si ottiene moltiplicando tra loro i contributi di ciascuna delle n coppie di variabili, quindi è pari a (π R2)n.
[18] Qua per trasformazione della meccanica si intende la trasformazione Tt associata ad un sistema anche più generale di quello definito dalle equazioni di Newton, ovvero un sistema Hamiltoniano dipendente dal tempo.