di Paul Lockhart
(Traduzione di Fausta Zibetti)

Questa è la traduzione integrale dell’articolo apparso con lo stesso titolo su XlaTangente n. 10 (pp. 38-43) e tratto da MAA Online (marzo 2008).

Per ulteriori informazioni visita http://www.maa.org/devlin/

Un musicista si risveglia da un terribile incubo. Nel suo sogno si è ritrovato in una società in cui l’educazione musicale è diventata obbligatoria. “Stiamo aiutando i nostri studenti a diventare più competitivi in un mondo sempre più pervaso dai suoni”. Gli educatori, i sistemi scolastici e lo Stato devono farsi carico di questo vitale progetto. Si affidano studi, si formano commissioni e si prendono decisioni - il tutto senza la consulenza o la partecipazione di un solo musicista o compositore in attività.

Dal momento che è noto che i musicisti sono soliti fissare le loro idee sugli spartiti musicali, questi curiosi segni neri e queste righe devono costituire il “linguaggio della musica”. È indispensabile che gli studenti acquisiscano dimestichezza con questo linguaggio se vogliono conseguire una qualunque certificazione di competenza musicale; in effetti, sarebbe assurdo attendersi che un bambino canti o suoni uno strumento senza possedere una completa formazione nella notazione musicale e nella teoria. Suonare e ascoltare la musica, per non parlare del comporre un brano originale, sono considerate materie molto avanzate e sono generalmente rinviate al college e più spesso all’università.

Sia per le scuole primarie che per quelle secondarie, l’obiettivo è allenare gli studenti a utilizzare questo linguaggio, a organizzare i simboli secondo una serie di regole predefinite: “La lezione di musica è il contesto nel quale prendiamo i nostri spartiti, i nostri insegnanti segnano alcune note sulla lavagna, e noi le ricopiamo o le trasponiamo in una chiave diversa. Dobbiamo accertarci di utilizzare correttamente le chiavi e le alterazioni in chiave, e i nostri insegnanti sono molto pignoli nel controllare che inseriamo tutte le semiminime. Una volta abbiamo dovuto risolvere un problema di scala cromatica e io l’ho risolto correttamente, ma il mio insegnante non mi ha dato un buon voto perché avevo disegnato le asticelle nel verso sbagliato.”

Nella loro saggezza, gli educatori si rendono presto conto che persino un bambino molto piccolo può recepire questo tipo di istruzione musicale. Effettivamente si considera abbastanza vergognoso che uno studente del terzo anno non abbia memorizzato completamente gli intervalli di quinta. “Devo cercare un insegnante di sostegno di musica per mio figlio. Non si impegna a svolgere i suoi compiti di musica. Dice che è noioso. Si limita a sedersi, a guardare fuori dalla finestra, a canticchiare tra sé le melodie, inventando motivetti sciocchi”.

Ai livelli più alti, la pressione aumenta. Dopo tutto, gli studenti devono essere preparati per i test nazionali e gli esami di ammissione al college. Gli studenti devono frequentare i corsi di Scale e Modi, di Metro, di Armonia e di Contrappunto. “Hanno davvero tanto da imparare, ma più tardi, al college, quando finalmente cominceranno ad ascoltare musica, apprezzeranno il lavoro che hanno fatto alle scuole superiori”. Naturalmente, pochi studenti continuano ad occuparsi di musica, così soltanto pochissimi riescono ad ascoltare i suoni che quei segni neri rappresentano. Nondimeno è importante che ciascun membro della società sia in grado di riconoscere una modulazione o un brano di fuga, anche se molti non ne ascolteranno mai uno. “A dire il vero, la maggior parte degli studenti non va molto bene in musica. Si annoiano in classe, le loro prestazioni sono molto scadenti, e i loro compiti sono a malapena leggibili. Non si interessano minimamente di quanto la musica sia importante nel mondo attuale; vogliono soltanto frequentare il minor numero possibile di corsi di musica e vogliono smettere di occuparsene. Immagino che vi siano persone portate per la musica e altre che non lo sono per nulla. Avevo un’allieva, ma, accidenti, quanto era eccezionale! I suoi spartiti erano impeccabili – ogni nota al posto giusto, calligrafia perfetta, diesis, bemolle, proprio bella. Sarebbe diventata una musicista straordinaria, un giorno”.

Risvegliandosi in un bagno di sudore freddo, il musicista si rende conto, per fortuna, che si era trattato solo di un folle sogno. “Naturalmente!” si rassicura, “Nessuna società ridurrebbe mai un’arte tanto bella e ricca di significato a qualcosa di così insensato e volgare; nessuna cultura può essere così crudele nei confronti dei suoi giovani da privarli di strumenti di comunicazione umana così naturali e appaganti. Che assurdità!”

Nel frattempo, all’altro capo della città, un pittore si è appena risvegliato da un sogno analogo…

Ero sorpreso di ritrovarmi in un’aula ordinaria, senza cavalletti né tubetti di colore. “Oh, non pratichiamo effettivamente la pittura fino alle scuole superiori” mi fu detto dagli studenti. “Al settimo anno studieremo prevalentemente i colori e gli strumenti”. Mi mostrarono un foglio da disegno. Su un lato c’erano campioni di colore ognuno con uno spazio libero a fianco. Dovevano scriverci i nomi dei colori corrispondenti. “Mi piace dipingere,” precisò uno di loro, “mi dicono che cosa fare e io lo faccio. È facile!”

Dopo la lezione parlai con l’insegnante. “Ma i vostri studenti non dipingono veramente? chiesi. “Beh, il prossimo anno incominceranno la Pre-Pittura-Con–I-Numeri. Questo li prepara alla più importante Pittura-Con-Le-Sequenze-Di-Numeri delle scuole superiori. Così inizieranno ad usare ciò che hanno imparato qui e lo applicheranno alle situazioni di pittura nella vita reale, intingendo il pennello nel colore, pulendolo, e cose del genere. Naturalmente noi teniamo conto delle capacità dei singoli studenti. I pittori davvero eccellenti – quelli che conoscono i loro colori e i loro pennelli in lungo e in largo – approdano alla pittura vera un po’ prima. E alcuni di essi frequentano persino le lezioni di Perfezionamento Avanzato per la promozione al college. Ma soprattutto noi cerchiamo di dare a questi ragazzi delle buone basi, così quando usciranno nel mondo reale e imbiancheranno la loro cucina non combineranno un pasticcio totale”.

“Ah, queste lezioni delle scuole superiori che hai nominato…”

“Intendi dire Pittura-Con-I-Numeri? Più tardi ti farò vedere l’incremento vertiginoso del numero di iscrizioni. Penso che sia dovuto, nella maggior parte dei casi, ai genitori che desiderano assicurarsi che il loro figlio frequenti un buon college. Niente fa più effetto di un Certificato Avanzato di Pittura-Con-I-Numeri in una pagella di scuola superiore.”.

“Perché ai college interessa se sai riempire delle aree numerate con il colore corrispondente?”

“Beh, sai, è indice di un pensiero chiaro e logico. E naturalmente se uno studente sta pensando di specializzarsi in una delle scienze visive, come moda o decorazione di interni, allora è veramente una buona idea quella di presentare i fondamenti di pittura acquisiti durante le scuole superiori.”.

“Capisco. E quando gli studenti dipingeranno liberamente, su una tela bianca?”

“Mi sembri uno dei miei insegnanti! Insistevano sull’espressione di sé, sui sentimenti e cose del genere – astrazioni davvero fuori moda. Io stesso ho un diploma in Pittura, ma, a dire il vero, non ho mai lavorato molto con le tele bianche. Ho utilizzato soltanto le scatole di Pittura-Con-I-Numeri fornite dal Ministero dell’Istruzione”.

***

Purtroppo, il nostro attuale sistema di formazione matematica ricalca esattamente questo genere di incubo. In effetti, se dovessi individuare un meccanismo pensato proprio per distruggere la naturale curiosità e l’amore per la creazione di schemi di qualsiasi bambino, non potrei far meglio di quanto non sia già stato fatto – semplicemente non avrei la fantasia che occorre per concepire quel genere di idee insensate e avvilenti per lo spirito che costituiscono l’attuale formazione matematica.

Tutti sanno che c’è qualcosa che non va. I politici dicono: “ci vogliono livelli più elevati”. Le scuole dicono: “abbiamo bisogno di maggiori risorse.” Gli educatori dicono una cosa e gli insegnanti ne dicono un’altra. Hanno tutti torto. Gli unici che capiscono veramente che cosa stia succedendo sono quelli che molto spesso vengono bistrattati e poco ascoltati: gli studenti. Essi dicono, “le lezioni di matematica sono stupide e noiose”, e hanno ragione.

 

Matematica e Cultura

La prima cosa da capire è che la matematica è un’arte. La differenza tra la matematica e le altre arti, quali la musica e la pittura, è che la nostra cultura non la riconosce come tale. Ognuno capisce che i poeti, i pittori e i musicisti creano opere d’arte, e si esprimono con parole, immagini e suoni. In realtà, la nostra società è piuttosto generosa nei confronti dell’espressione creativa; architetti, cuochi e persino registi televisivi sono considerati artisti. E allora, perché non i matematici?

Una parte del problema sta nel fatto che nessuno ha la più pallida idea di che cosa facciano i matematici. Comunemente si pensa che abbiano qualcosa a che fare con la scienza: forse aiutano gli scienziati con le loro formule o, forse, per una ragione o per un’altra, riempiono i computer con grandi numeri. Non c’è dubbio che se il mondo dovesse essere diviso in “poetici sognatori” e “pensatori razionali”, la maggioranza delle persone collocherebbe i matematici nella seconda categoria.

Tuttavia, il fatto è che non c’è nulla di così onirico e poetico, nulla di così radicale e sovversivo, e psichedelico, quanto la matematica. È tanto spiazzante quanto la cosmologia o la fisica (i matematici concepirono i buchi neri molto prima che gli astronomi ne trovassero realmente qualcuno), e consente maggiore libertà di espressione della poesia, dell’arte o della musica (che dipendono pesantemente dalle proprietà dell’universo fisico). La Matematica è la più pura delle arti, ed è anche la più incompresa.

Perciò cercherò di spiegare che cos’è la matematica e che cosa fanno i matematici. Non c’è niente di meglio che iniziare con un’eccellente descrizione di G. H. Hardy:

Un matematico, come un pittore o un poeta, è un

creatore di schemi. Se i suoi schemi risultano più durevoli

di quelli dei primi, è perché sono fatti di idee.

Così i matematici si ritrovano tra loro per creare schemi di idee. Che genere di schemi? Che genere di idee? Idee sui rinoceronti? No, quelle le lasciamo ai biologi. Idee sul linguaggio e sulla cultura? Di solito no. Queste cose sono troppo complicate per i gusti della maggior parte dei matematici. Se c’è qualcosa di simile a un principio estetico unificante in matematica, questo è: semplice è bello. Ai matematici piace riflettere sulle cose più semplici possibili, e le cose più semplici possibili sono immaginarie.

Per esempio, se ho voglia di riflettere sulle forme – e mi capita spesso – potrei immaginare un triangolo inscritto in un rettangolo:

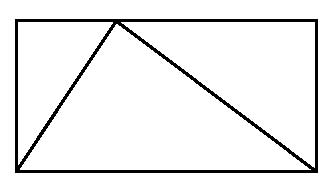
Mi domando: il triangolo quanta parte occupa della superficie del rettangolo? I due terzi? La cosa importante da capire è che non sto parlando di questo disegno di un triangolo inscritto in un rettangolo. Non sto neppure parlando di qualche triangolo di metallo nel sistema di travi di un ponte. Non c’è alcun secondo fine pratico qui. Sto solo giocando. Proprio in questo consiste la matematica: porre delle domande, giocare, divertirsi con la propria immaginazione. Per un verso, la domanda su quanta parte della superficie del rettangolo è occupata dal triangolo non ha alcun senso se la si riferisce a oggetti reali e concreti. Un triangolo concreto, per quanto sia stato realizzato con cura, è pur sempre un aggregato, irrimediabilmente complicato, di atomi che si muovono: cambia le sue dimensioni da un minuto all’altro. A meno che non vogliate parlare di qualche genere di misure approssimate. Bene, ecco dove l’estetica entra in gioco. Il problema concreto non è affatto semplice, e dipende da ogni genere di dettaglio del mondo reale. Lasciamolo agli scienziati. Il problema matematico riguarda un triangolo immaginario inscritto in un rettangolo immaginario. I lati sono perfetti perché io voglio che lo siano: questo è il tipo di oggetto su cui preferisco riflettere. E questo è il cuore della matematica: le cose sono ciò che tu vuoi che siano. Tu hai una scelta illimitata; non c’è alcuna realtà che interferisca con te.

D’altra parte, dopo che tu hai fatto le tue scelte (per esempio, potrei scegliere di volere che il mio triangolo sia isoscele, oppure no), le tue nuove creazioni fanno ciò che vogliono, che ti piaccia o no. Questo è il dato sorprendente dei modelli immaginari: ti rispondono! Il triangolo occupa una certa superficie del suo rettangolo, ma io non ho alcun controllo su quanto tale superficie sia estesa. C’è un numero là fuori, forse è due terzi, forse non lo è, ma non sono in grado di dire a che cosa corrisponda. Io devo scoprire a che cosa corrisponde.

Così dobbiamo giocare e immaginare in libertà, realizzare schemi e porci delle domande su di essi. Ma come facciamo a rispondere a queste domande? Non è affatto come per la scienza. Non c’è alcun esperimento che possiamo fare con provette, strumenti e cose simili che ci diranno la verità su un prodotto della nostra immaginazione. L’unico modo per arrivare a questa verità è proprio quello di usare la nostra immaginazione: ed è una faccenda complicata.

Nel caso del triangolo inscritto nel suo rettangolo, arrivo a vedere qualcosa di semplice e bello:

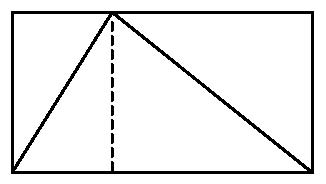
Se divido il rettangolo in due parti nel modo della figura qui sopra, posso osservare che ciascuna parte è divisa diagonalmente a metà dai lati del triangolo. Perciò lo spazio all’interno del triangolo è pari a quello che sta all’esterno. Ciò significa che il triangolo deve occupare esattamente la metà del rettangolo! (Ecco così qualcosa che può dare l’idea di che cos’è un pezzo di matematica. E anche il breve racconto che l’accompagna dà un esempio dell’arte del matematico: porsi semplici ed eleganti domande sulle nostre creazioni immaginarie, e ingegnarci a trovare spiegazioni soddisfacenti e belle. Non vi è nulla che si avvicini meglio al regno dell’idea pura; è affascinante, è divertente, ed è libero!)

Ora, da dov’è nata questa mia idea? Come facevo a sapere di dover disegnare quella linea? Come fa un pittore a sapere dove appoggiare il pennello? Ispirazione, esperienza, tentativi ed errori, pura fortuna. Questa è la sua arte, creare queste brevi poesie di pensiero, questi sonetti di pura razionalità. C’è un meraviglioso fluire in questa forma d’arte. La relazione tra il triangolo e il rettangolo era un mistero, e poi proprio quella breve linea l’ha svelato. Non riuscivo a vedere, poi tutto ad un tratto ci sono riuscito. In qualche modo, sono stato in grado di creare dal nulla una bellezza profonda e semplice, e in questo processo ho mutato me stesso. Non è forse questa l’essenza dell’arte?

Questo è il motivo per cui è così sconfortante vedere ciò che è stato fatto alla matematica a scuola. Una ricca e affascinante avventura dell’immaginazione è stata ridotta ad una sterile sequenza di “dati di fatto” da memorizzare e di procedure da seguire. Invece di una semplice e naturale domanda sulle forme, e di un processo creativo e gratificante di invenzione e scoperta, gli studenti sono alle prese con questo:

 

Formula dell’area del triangolo: A=½b·h

           

“L’area del triangolo è uguale a base per altezza diviso due”. Agli studenti si chiede di memorizzare questa formula e poi di “applicarla” ripetutamente negli “esercizi”. Se ne vanno così il brivido, la gioia, persino il dolore e la frustrazione dell’atto creativo. Non c’è più neppure un problema. La domanda è stata posta e al tempo stesso le è stata data una risposta – allo studente non è rimasto più niente da fare.

Ora, permettetemi di essere chiaro. Non è certo sulle formule, o sul memorizzare fatti interessanti che sto facendo obiezioni. Sono importanti in alcune situazioni e hanno tanto senso quanto ne ha lo studio di un vocabolario: ti aiuta a creare opere d’arte più elaborate e più ricche di sfumature. Ma non è il fatto che il triangolo occupi metà dell’area del rettangolo ciò che importa. L’interesse sta nella bella idea di dividerlo con una linea e nel modo in cui tale idea ne può ispirare altre e può farci fare passi avanti significativi in altri, diversi problemi: qualcosa che una semplice presa d’atto dei fatti non darà mai.

Eliminare il processo creativo e lasciarne solo i risultati ha come sicura conseguenza il fatto che nessuno potrà mai sentirsi coinvolto nella questione. È come dire che Michelangelo ha creato una bella scultura, senza farla vedere. Come posso pensare di esserne ispirato? (Anzi, è molto peggio di così: almeno, in quel caso è sottinteso che c’è un’arte della scultura che mi viene impedito di apprezzare).

Se ci si concentra sul che cosa, e si tralascia il perché, la matematica si riduce a un guscio vuoto. L’arte non sta nella “verità”, ma nella spiegazione, nella dimostrazione. È la dimostrazione stessa che assegna un contesto alla verità, e definisce che cosa è stato realmente detto e inteso. La matematica è l’arte della spiegazione. Se si nega agli studenti l’opportunità di intraprendere questa attività – porsi i propri problemi, elaborare le proprie congetture e le proprie scoperte, sbagliare, essere creativamente frustrati, avere un’ispirazione, e mettere insieme le proprie personali spiegazioni e prove – si nega loro la matematica stessa. Perciò no, non mi sto lamentando della presenza dei fatti e delle formule nei nostri corsi di matematica, mi sto lamentando della mancanza della matematica nei nostri corsi di matematica.

Se il vostro insegnante di arte vi dicesse che la pittura consiste nel riempire delle aree numerate, capireste che c’è qualcosa che non va. Il sistema culturale vi informa – ci sono i musei e le gallerie e c’è dell’arte anche in casa vostra. La pittura è a ragione considerata dalla società come un mezzo di espressione umana. Parimenti, se il vostro insegnante di scienze cercasse di convincervi che l’astronomia consiste nel predire il futuro di una persona basandosi sulla sua data di nascita, pensereste che è matto – la scienza è penetrata nella cultura a tal punto che quasi tutti sanno qualcosa di atomi, di galassie e di leggi della natura. Ma se il vostro insegnante di matematica vi dà l’impressione, sia esplicitamente che implicitamente, che la matematica consista in formule e definizioni e nel memorizzare algoritmi, chi vi raddrizzerà?

Il problema culturale è un mostro che si autoriproduce: gli studenti imparano la matematica dai loro insegnanti, e gli insegnanti la imparano dai loro insegnanti, così la mancanza di comprensione e di apprezzamento per la matematica nella nostra cultura si replica all’infinito. Anzi, peggio, la perpetuazione di questa “pseudo-matematica”, questa enfasi sulla manipolazione accurata e senza senso di simboli, crea la sua propria cultura e il suo peculiare sistema di valori. Coloro che vi si sono assuefatti ricavano dal proprio successo una straordinaria autostima. L’ultima cosa che vorrebbero sentirsi dire è che la matematica ha a che fare davvero con la creatività naturale e con la sensibilità estetica. Molti studenti universitari ci sono rimasti male quando hanno scoperto, dopo dieci anni durante i quali si sono sentiti ripetere che erano “bravi in matematica”, che in realtà non avevano alcun vero talento matematico ed erano semplicemente bravi a seguire delle indicazioni. La matematica non consiste nel seguire delle indicazioni, consiste nel trovare nuove vie.

E non ho neppure accennato alla mancanza di critica matematica nella scuola. Agli studenti non è mai stato rivelato il segreto che la matematica, come la letteratura, è creata dagli esseri viventi per il proprio piacere; che le attività della matematica sono soggette al giudizio critico, che ciascuno può possedere e sviluppare un gusto matematico. Un frammento di matematica è come una poesia, e noi possiamo domandarci se soddisfa i nostri criteri estetici: è fondata questa dimostrazione? Ha senso? È semplice ed elegante? Mi conduce sempre più vicino al cuore del problema? Naturalmente non si pratica alcuna critica a scuola – non c’è alcuna arte da sottoporre a giudizio critico!

Perché non vogliamo che i nostri ragazzi imparino la matematica? Forse perché non abbiamo fiducia in loro, perché pensiamo che sia troppo difficile? Abbiamo la sensazione che siano in grado di elaborare ragionamenti e di trarre le proprie conclusioni su Napoleone, e allora perché non sui triangoli? Penso che ciò avvenga semplicemente perché per cultura noi ignoriamo che cosa sia la matematica. L’impressione che ne stiamo dando è che sia qualcosa di molto freddo e particolarmente tecnico, che nessuno può mai comprendere – una profezia compiuta in se stessa, se mai ce ne fosse una.

Sarebbe abbastanza spiacevole se la cultura ignorasse del tutto la matematica, ma ciò che è persino peggio è che ora la gente pensa di sapere che cos’è la matematica – ed evidentemente è vittima dell’equivoco che la matematica sia in qualche misura utile alla società! Questa è in effetti una enorme differenza tra la matematica e le altre arti. La matematica è vista dalla cultura come una specie di strumento funzionale alla scienza e alla tecnologia. Tutti sanno che la poesia e la musica sono concepite per il puro divertimento e per l’esaltazione dello spirito umano (e da qui segue la loro virtuale eliminazione dal curriculum delle scuole di stato). Invece no, la matematica è…  importante.

SIMPLICIO:      Stai davvero cercando di sostenere che la matematica non offre alcuna applicazione utile o pratica alla società?

SALVIATI:        Naturalmente no. Sto semplicemente suggerendo che solo perché capita che qualcosa abbia conseguenze pratiche, ciò non significa che si esaurisca in questo. La musica può incitare gli eserciti alla battaglia, ma non è questo il motivo per cui si scrivono sinfonie. Michelangelo ha decorato una volta, ma sono sicuro che avesse in mente altre cose più nobili.

SIMPLICIO:     Ma non ci serve forse che la gente impari queste utili applicazioni della matematica? Non ci servono anche contabili, carpentieri e gente di questo tipo?

SALVIATI:        Quante persone credi che utilizzino davvero questa “matematica pratica” che avrebbero imparato a scuola? Pensi che quei carpentieri là fuori utilizzino la trigonometria? Quanti adulti si ricordano come dividere le frazioni, o risolvere un’equazione di secondo grado? Ovviamente l’attuale programma di esercitazioni pratiche non sta funzionando, e per una valida ragione: è terribilmente noioso e nessuno lo userebbe comunque. Perciò, perché la gente pensa che sia così importante? Non vedo quale vantaggio vi sia per una società nel fatto che tutti i suoi membri se ne vadano in giro portando con sé vaghe memorie di formule algebriche e figure geometriche, e il chiaro ricordo di averle odiate. Potrebbe portare qualche vantaggio, invece, mostrare loro qualcosa di bello e dare loro l’opportunità di apprezzare il fatto di essere creativi, flessibili, pensatori dalle larghe vedute – quel genere di cose che una vera educazione matematica dovrebbe fornire.

SIMPLICIO:      Ma la gente ha bisogno di sapere come far quadrare il proprio bilancio, sei d’accordo?

SALVIATI:        Sono sicuro che la maggior parte della gente usa la calcolatrice per i calcoli di ordinaria amministrazione. E perché no? È certamente più facile e più affidabile. Ciò che voglio dire non è solo che il sistema attuale è terribilmente sbagliato, ma piuttosto che ciò che manca è terribilmente bello! La Matematica dovrebbe essere insegnata come arte per l’arte. Questi aspetti di “utilitarismo” mondano seguirebbero in modo del tutto naturale come un banale sottoprodotto. Beethoven avrebbe potuto facilmente scrivere un motivetto pubblicitario, ma la motivazione che l’ha spinto era il desiderio di creare qualcosa di bello.

SIMPLICIO:      Ma non tutti sono nati per essere artisti. Che cosa ne sarà di quei ragazzi che non sono “portati per la matematica”? Come si collocano all’interno del tuo schema?

SALVIATI:        Se ciascuno fosse “esposto alla matematica” al suo stato naturale, con tutte le sfide, il divertimento e le sorprese che essa implica, penso che potremmo vedere un radicale cambiamento sia nell’atteggiamento degli studenti verso la matematica sia nella nostra idea di ciò che significa “essere bravi in matematica”. Facendo come facciamo, stiamo perdendo tanti matematici potenzialmente dotati - persone creative, intelligenti che giustamente rifiutano ciò che sembra una materia insensata e sterile. Sono semplicemente troppo intelligenti per perdere tempo con tali sciocchezze.

SIMPLICIO:      Ma non pensi che se i corsi di matematica fossero gestiti più come i corsi di arte, un sacco di allievi non imparerebbe nulla?

SALVIATI:        Non stanno imparando nulla già ora! Meglio non avere alcun corso di matematica piuttosto che fare ciò che si fa oggi. Almeno alcune persone potrebbero avere la fortuna di imparare da sole qualcosa di bello.

SIMPLICIO:      Così elimineresti la matematica dal curriculum scolastico?

SALVIATI:        La matematica è già stata eliminata! L’unica domanda è che cosa fare del guscio insulso e vuoto che rimane. Naturalmente preferirei sostituirlo con un coinvolgimento attivo e gioioso nelle idee matematiche.

SIMPLICIO:       Ma quanti sono gli insegnanti che abbiano sufficiente dimestichezza con la loro materia per insegnarla così?

SALVIATI:        Molto pochi. E questa è soltanto la punta dell’iceberg…

 

La Matematica a Scuola

Certamente non c’è modo più sicuro per uccidere l’entusiasmo e l’interesse in una disciplina che renderla un elemento obbligatorio del curriculum scolastico. Includetela tra le materie più importanti delle prove di verifica standardizzate e potete star sicuri che il sistema educativo le risucchierà l’anima. I comitati scolastici non capiscono che cosa sia la matematica, e non lo capiscono nemmeno gli educatori, gli autori dei libri di testo, le case editrici, e purtroppo, neppure la maggior parte dei nostri insegnanti di matematica. La portata del problema è così grande che non so davvero da dove cominciare.

Cominciamo con il fallimento della “riforma della matematica”. Per molti anni c’è stata una crescente consapevolezza che qualcosa non andasse nell’educazione matematica. Sono stati commissionati studi, sono state organizzate conferenze, e innumerevoli commissioni di insegnanti, editori di libri di testo, ed educatori (qualunque cosa essi siano) sono stati formati per “risolvere il problema”. Tralasciando l’atteggiamento interessato rivolto alla riforma da parte dell’industria libraria (che trae profitto da ogni minima oscillazione politica offrendo “nuove” edizioni delle sue illeggibili mostruosità), l’intero movimento riformatore ha sempre mancato il vero problema. Il curriculum di matematica non necessita di essere riformato, necessita di essere smantellato.

Tutto questo affannarsi e lavorare sui minimi dettagli di quali “argomenti” dovrebbero essere insegnati in quale ordine, o sull’uso di questa simbologia invece di quell’altra, o su quale tipo e modello di calcolatore usare, per l’amor di Dio – è come cercare di riparare i posti in coperta sul Titanic! La matematica è la musica della ragione. Fare matematica significa impegnarsi in un atto di scoperta e congettura, intuizione ed ispirazione; trovarsi in uno stato confusionale (non perché non riesci a trovarci un senso, ma perché tu le hai dato un senso e ancora non capisci che cosa stia combinando la tua creazione) avere un’idea originale; essere frustrato come un artista; essere sgomento e travolto da una bellezza per così dire dolorosa; essere vivo, accidenti. Rimuovete questo dalla matematica e potrete tenere tutte le conferenze che volete; non servirà. Operate come volete, dottori: il vostro paziente è già morto.

L’aspetto più triste di questa “riforma” sono i tentativi per “rendere interessante la matematica” e “importante per la vita dei ragazzi”. Non c’è bisogno di rendere la matematica interessante – è già più interessante di quanto possiamo immaginare! E il suo vanto è la sua completa irrilevanza per la nostra vita. Per questo è così divertente!

Cercare di presentare la matematica come importante per la vita quotidiana inevitabilmente appare forzato e innaturale: “Vedete, ragazzi; se conoscete l’algebra, allora potete ricavare quanti anni ha Maria se sappiamo che ha due anni in più del doppio della sua età di sette anni fa!” (Come se qualcuno potesse mai aver accesso a questo ridicolo tipo di informazioni, e non alla sua età.) L’algebra non riguarda la vita quotidiana, riguarda i numeri e le simmetrie – e questa è un’occupazione che ha valore in se stessa:

Supponiamo che io abbia la somma e la differenza di due numeri. Come posso ricavare quali siano questi numeri?

Ecco un quesito semplice ed elegante, e non richiede alcuno sforzo per essere reso attraente. Gli antichi Babilonesi si divertivano a lavorare con tali problemi, e lo stesso vale per i nostri studenti. (E spero che anche a voi piaccia riflettere su di essi!) Non dobbiamo farci in quattro per dare importanza alla matematica. Essa ha importanza esattamente come ce l’ha ogni arte: per il fatto di essere un’esperienza umana significativa.

In ogni caso, pensate veramente che i ragazzi vogliano proprio qualcosa che sia importante per la loro vita quotidiana? Pensate che qualcosa di pratico come l’interesse composto li ecciterà? Alla gente piace la fantasia, e questo è proprio ciò che la matematica può dare – uno stacco dalla vita quotidiana, un sollievo dal mondo del lavoro pragmatico di ogni giorno.

Un problema simile si presenta quando gli insegnanti o i libri di testo soccombono alla ”carineria”. È qui che, nel tentativo di combattere la cosiddetta “ansia matematica” (uno degli innumerevoli disagi che sono effettivamente causati dalla scuola), la matematica viene resa “amichevole”. Per aiutare i vostri studenti a memorizzare le formule dell’area e della circonferenza di un cerchio, per esempio, potreste inventare questa storia del signor C, che porta a spasso la signora A e le racconta come è bello il suo “due-pigreco-erre” (C=2πr) e lei gli racconta del suo “pigreco-erre-quadro” ( A=πr²) [giochi di parole basati sulla identica pronuncia della lettera “r” e del verbo “are” e della lettera “pi” e del sostantivo “pie”, torta, impossibili da rendere in italiano, N.d.T.] o simili sciocchezze. Ma che dire della storia vera? Quella della sfida dell’umanità al problema di misurare le curve; di Eudosso e Archimede e del metodo di esaustione, sulla trascendenza di pigreco? Che cosa è più interessante: misurare le semplici dimensioni di una porzione circolare di carta disegnata, usando una formula che qualcuno vi ha fornito senza spiegazione (e vi ha costretto a memorizzare e ad applicare in continuazione) o ascoltare la storia di uno dei problemi più belli ed affascinanti, e una delle più brillanti e potenti idee della storia dell’umanità? Noi stiamo uccidendo l’interesse della gente per i cerchi, accidenti!

Perché non stiamo dando ai nostri studenti la possibilità almeno di ascoltare queste cose, anche senza dar loro un’opportunità di fare davvero matematica, e di farsi avanti con le loro idee personali, con le loro opinioni e le loro reazioni? Quale altra materia è abitualmente insegnata senza alcun accenno alla sua storia, alla sua filosofia, al suo sviluppo tematico, ai suoi criteri estetici, e al suo stato attuale? Quale altra materia rifugge dalle sue fonti primarie – belle opere d’arte di qualcuna delle menti più creative della storia – a vantaggio dell’imbastardimento di terza categoria dei libri di testo?

 

Il problema principale della matematica scolastica è che non ci sono problemi. Oh, conosco quelli che vengono fatti passare per problemi nelle lezioni di matematica, questi insipidi “esercizi”. “Ecco un tipo di problema. Ecco come risolverlo. Sì, sarà oggetto di verifica. Fate gli esercizi dispari dall’1 al 35 come compito”. Che modo triste per imparare la matematica: essere uno scimpanzé ammaestrato.

Ma un problema, una genuina naturale umana domanda – quella è un’altra cosa. Quanto è lunga la diagonale di un cubo? I numeri primi sono infiniti? L’infinito è un numero? In quanti modi posso ricoprire simmetricamente una superficie? La storia della matematica è la storia del coinvolgimento del genere umano in domande come queste, non il folle rigurgito di formule e di algoritmi (con l’aggiunta di esercizi forzati inventati per prendere pratica).

Un buon problema è qualcosa che non si sa come risolvere. Questo è ciò che lo rende un buon gioco ad incastro, e una bella opportunità. Un buon problema non si limita a rimanersene lì isolato, ma serve come trampolino per altre interessanti domande. Un triangolo occupa la metà del suo rettangolo. Che cosa dire di una piramide inscritta nel suo parallelepipedo rettangolo? Possiamo trattare questo problema allo stesso modo?

Posso capire l’idea di allenare gli studenti a padroneggiare determinate regole - anch’io lo faccio. Ma non fine a se stessa. Le tecniche in matematica, come in qualunque arte, devono essere apprese all’interno di un contesto. I grandi problemi, la loro storia, il processo creativo – questo è il giusto ambito. Date ai vostri studenti un buon problema, lasciateli lottare e subire frustrazioni. Osservate a che risultati arrivano. Aspettate fino a quando stanno morendo per un’idea, allora dategli un po’ di tecniche. Ma non troppe.

Allora lasciate da parte i vostri programmi e le vostre lavagne luminose, i vostri abominevoli e coloratissimi libri di testo, i vostri CD-rom e tutto l’equipaggiamento di quel bizzarro spettacolo da circo itinerante che è l’educazione contemporanea, e fate semplicemente matematica con i vostri studenti! Gli insegnanti di arte non sprecano il loro tempo con libri di testo e meccanici esercizi su tecniche specifiche. Fanno ciò che è naturale per la loro materia: fanno dipingere i ragazzi. Vanno di cavalletto in cavalletto, dando suggerimenti e offrendo indicazioni:

“Stavo pensando al nostro problema del triangolo, e ho notato una cosa. Se il triangolo è veramente inclinato, allora non occupa la metà del suo rettangolo! Guarda:

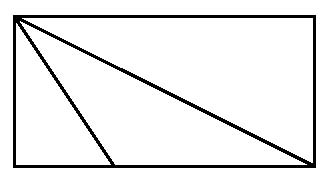
“Eccellente osservazione! La nostra dimostrazione del taglio parte dal presupposto che il vertice del triangolo sia posto perpendicolarmente sopra la base. Ora ci serve una nuova idea”.

“Dovrei cercare di tagliarlo in un altro modo?”

“Certamente. Prova ogni tipo di idea. Fammi sapere a che risultato arrivi!”.

Perciò, come dobbiamo insegnare ai nostri studenti a fare matematica? Scegliendo problemi impegnativi e naturali adatti ai loro gusti, alla loro personalità, e al loro livello di esperienza. Dando loro il tempo di fare delle scoperte e di formulare congetture. Aiutandoli a perfezionare i loro ragionamenti e creando un’atmosfera di salutare e vibrante spirito critico matematico. Mostrandosi flessibili e aperti ad improvvisi mutamenti di direzione verso i quali può portare la loro curiosità. In breve, avendo un rapporto intellettuale onesto con i nostri studenti e con la nostra materia.

Ovviamente ciò che sto suggerendo è impossibile per un certo numero di motivi. Anche tralasciando il fatto che i curricula statali e le prove standardizzate di valutazione di fatto eliminano l’autonomia dell’insegnante, dubito che la maggior parte degli insegnanti voglia instaurare un rapporto così intenso con i suoi studenti. Richiede troppa vulnerabilità e troppa responsabilità – in breve, troppo lavoro!

È molto più facile essere un passivo veicolo di alcuni “materiali” pubblicati e seguire le istruzioni da flacone di shampoo “lettura, verifica, ripetizione” che non riflettere profondamente e intensamente sul significato della propria materia e su come sia meglio trasmettere tale significato direttamente e onestamente ai propri studenti. Noi siamo incoraggiati a evitare il difficile compito di prendere decisioni basate sulla nostra saggezza individuale e sulla nostra coscienza, e ad “andare avanti con il programma”. È semplicemente il cammino di minor resistenza:

            i LIBRI DI TESTO stanno agli  INSEGNANTI come

le case farmaceutiche stanno ai medici

le case discografiche stanno ai disk jockey

le corporation stanno ai membri del Congresso.

Il guaio è che la matematica, come la pittura e la poesia, è un duro lavoro creativo. Il che la rende molto difficile da insegnare. La matematica è un processo lento e contemplativo. Realizzare un’opera d’arte richiede tempo, e ci vuole un abile insegnante per riconoscerne una. Naturalmente è più facile dettare una serie di regole che guidare giovani aspiranti artisti, ed è più facile scrivere il manuale di un videoregistratore che scrivere un vero e proprio libro con un punto di vista.

La matematica è un’arte, e l’arte dovrebbe essere insegnata da artisti in attività oppure  almeno da persone che apprezzano la forma dell’arte e possono riconoscerla quando la vedono. Non è necessario che tu impari la musica da un compositore professionista, ma vorresti che a te o a tuo figlio venisse insegnata da qualcuno che non sa suonare neppure uno strumento e che non ha mai ascoltato un brano di musica in vita sua? Accetteresti come insegnante di arte qualcuno che non abbia mai preso in mano una matita o non abbia mai messo piede in un museo? Perché dunque accettiamo insegnanti di matematica che non hanno mai prodotto un pezzo originale di matematica, che non sanno nulla della storia o della filosofia della materia, nulla dei recenti sviluppi, nulla in concreto oltre a quello che sono tenuti a presentare ai loro sfortunati studenti? Che razza di insegnante è questo? Come si può insegnare qualcosa che non si fa in prima persona? Non so ballare, e di conseguenza non avrò mai la presunzione di pensare di poter tenere una lezione di danza (posso provarci, ma non sarebbe bello). La differenza è che io so di non saper ballare. Nessuno mi ha detto che sono un bravo ballerino solo perché conosco una manciata di termini relativi alla danza.

Ora non sto dicendo che gli insegnanti di matematica debbano essere matematici professionisti – lungi da me. Ma non dovrebbero almeno capire che cosa sia la matematica, essere bravi e provare piacere nel farla?

Se l’insegnamento è ridotto a mera trasmissione di dati, se non c’è condivisione di entusiasmo e di meraviglia, se gli insegnanti stessi sono ricettori passivi di informazioni e non creatori di nuove idee, che speranza c’è per i loro studenti? Se sommare frazioni è per un insegnante un’arbitraria serie di regole, e non il risultato di un processo creativo e il risultato di scelte estetiche e di desideri, allora ovviamente sarà lo stesso anche per i poveri studenti.

L’insegnamento non riguarda l’informazione. Consiste nell’avere un rapporto intellettuale onesto con i propri studenti. Non richiede alcun metodo, nessuno strumento, e nessun allenamento. Soltanto la capacità di essere veri. E se non si può essere veri, allora non si ha alcun diritto di accanirsi su ragazzini innocenti.

In particolare non si può insegnare ad insegnare. Le scuole di formazione sono completamente fallite. Oh, si possono prendere lezioni sullo sviluppo della prima infanzia e cose del genere, e ci si può allenare ad usare una lavagna “efficacemente” e a preparare un’organizzata “programmazione di una lezione” (il che, tra l’altro, assicura che la vostra lezione sarà programmata, e perciò falsa), ma non sarete mai un vero insegnante se non siete in grado di essere persone vere. Insegnare significa apertura e onestà, capacità di trasmettere entusiasmo, e amore per l’apprendimento. Senza queste cose tutti i titoli di studio del mondo non vi aiuteranno, e in presenza di queste cose, essi sono completamente superflui.

È perfettamente semplice. Gli studenti non sono alieni. Essi reagiscono alla bellezza e agli schemi, e sono curiosi per natura come chiunque altro. Provate soltanto a parlare con loro! E, cosa ancor più importante, ascoltateli!

SIMPLICIO:      Bene, capisco che c’è un’arte nella matematica e che noi non stiamo facendo un buon lavoro di avvicinamento del pubblico ad essa. Ma questa non è una cosa piuttosto esoterica ed intellettuale da chiedere al nostro sistema scolastico? Non stiamo cercando di creare dei filosofi qui, vogliamo soltanto persone che abbiano una ragionevole padronanza dell’aritmetica di base così da poter operare nella società.

SALVIATI:        Ma questo non è vero! La stessa matematica scolastica ha a che fare con molte cose che non hanno nulla da spartire con la capacità di operare in società – algebra e trigonometria, per esempio. Questi studi sono del tutto irrilevanti per la vita quotidiana. Sto semplicemente suggerendo che se abbiamo intenzione di inserire queste cose nella formazione di base di un grande numero di studenti, almeno facciamolo in modo organico e naturale. Inoltre, come ho detto prima, solo perché capita che una materia abbia qualche utilità mondana e pratica, ciò non significa che dobbiamo far diventare questa utilità il punto centrale del nostro insegnamento e apprendimento. Può essere vero che devi essere capace di leggere per poter compilare i moduli agli uffici della Motorizzazione, ma questo non è il motivo per cui si insegna a leggere ai bambini. Insegniamo loro a leggere per uno scopo più elevato: permettere loro l’accesso a idee belle e ricche di significato. Non solo sarebbe crudele insegnare a leggere in questo modo, costringendo ragazzini del terz’anno a compilare moduli delle ordinazioni e delle tasse:  non funzionerebbe! Noi impariamo le cose perché ci interessano nell’immediato, non perché potrebbero tornarci utili un domani. E invece questo è ciò che stiamo chiedendo ai ragazzi di fare con la matematica.

SIMPLICIO:      Ma non ci serve che i ragazzini del terz’anno siano in grado di usare l’aritmetica?

SALVIATI:        Perché? Vuoi che si allenino a calcolare quanto fa 427 più 389? Non è certo una domanda che molti ragazzini di otto o nove anni si stanno facendo. Analogamente, molti adulti non capiscono pienamente il valore dell’aritmetica dei numeri decimali eppure tu ti aspetti che dei ragazzini di terza ne abbiano un’idea chiara? Oppure non ti importa se la capiscono? È semplicemente troppo presto per questo genere di allenamento tecnico. Naturalmente si può fare, ma credo che in ultima analisi possa fare più male che bene. Molto meglio aspettare fino a quando la loro naturale curiosità riguardo ai numeri si manifesterà.

SIMPLICIO:      Allora che cosa dovremmo fare con i bambini durante le lezioni di matematica?

SALVIATI:        Giocate! Insegnate loro gli Scacchi, Go [gioco simile agli scacchi, N.d.T], Hex e Backgammon, Sprouts e Nim, qualunque cosa. Inventate un gioco. Fate dei puzzle. Esponeteli a situazioni in cui sia necessario usare il ragionamento deduttivo. Non preoccupatevi dei simboli e delle tecniche di calcolo, aiutateli a diventare pensatori matematici attivi e creativi.

SIMPLICIO:      Mi sembra che stiamo correndo un terribile rischio. Che cosa accadrebbe se noi riducessimo l’importanza dell’aritmetica al punto che i nostri studenti finissero per non essere più capaci di addizionare e sottrarre?

SALVIATI:        Penso che il rischio di gran lunga più grande sia quello di creare scuole prive di qualunque genere di espressione creativa, in cui la funzione degli studenti sia quella di memorizzare dati, formule e liste di vocaboli, e poi di rigurgitarli in prove di verifica standardizzate – “Preparare oggi la forza lavoro di domani!”

SIMPLICIO:      Ma certamente c’è qualche corpus di fatti matematici di cui una persona istruita dovrebbe essere a conoscenza.

SALVIATI:        Sì, il più importante dei quali è che la matematica è una forma d’arte donata agli esseri umani per il loro piacere! Giusto, sì, sarebbe bello se la gente conoscesse alcune cose basilari sui numeri o sulle forme, per esempio. Ma ciò non si otterrà mai con una sequenza meccanica: memorizzazione - esercizi orali – lezioni – esercizi scritti. Le cose si imparano facendole e si ricorda ciò che interessa. Abbiamo milioni di adulti che se ne vanno in giro con la formula “meno b, più o meno radice quadrata di b alla seconda meno 4ac, tutto diviso 2a” nella loro testa, e non hanno assolutamente idea di che cosa voglia dire. E il motivo è che non è mai stata data loro la possibilità di scoprire o inventare da sé cose del genere. Non hanno mai avuto un problema impegnativo con cui cimentarsi, da cui essere frustrati, e che abbia fatto nascere in loro il desiderio di tecniche e di metodi. Non è mai stata raccontata loro la storia del rapporto del genere umano con i numeri – nessuna tavoletta con antichi problemi babilonesi, nessun Rhind Papyrus, nessun Liber Abaci, nessuna Ars Magna. E, cosa più importante, nessuna opportunità per loro di provare interesse per una domanda; era già stata risolta prima ancora che potessero formularla.

SIMPLICIO:      Ma non abbiamo il tempo perché ciascuno studente si inventi da sé la matematica! Ci sono voluti secoli perché qualcuno scoprisse il Teorema di Pitagora. Come ci si può aspettare che un comune ragazzino lo faccia?

SALVIATI:        Non me l’aspetto. Voglio essere chiaro su questo punto. Mi sto lamentando della totale assenza di arte e di invenzione, storia e filosofia, contesto e prospettiva dal curriculum di matematica. Ciò non significa che i simboli, le regole e lo sviluppo di una conoscenza di base non abbiano un posto. Ovviamente ce l’hanno. Dovremmo avere però tutto. Se obietto ad un pendolo di essere troppo spostato da un lato, non significa che voglio che si sposti tutto dall’altro lato. Ma il fatto è che si impara meglio quando il risultato deriva da un processo. Un concreto apprezzamento per la poesia non discende dal memorizzare una manciata di poesie, deriva dallo scriverne di proprie.

SIMPLICIO:      Sì, ma prima di poter scrivere le proprie poesie, si deve imparare l’alfabeto. Il processo deve pur cominciare da qualche parte. Bisogna imparare a camminare prima di poter correre.

SALVIATI:        No, bisogna avere qualcosa verso cui correre. I bambini sanno scrivere poesie e storie non appena imparano a leggere e scrivere. Un brano di scrittura di un bambino di sei anni è una cosa meravigliosa, e l’ortografia e gli errori di punteggiatura non lo rendono meno bello. Persino i bambini molto piccoli sanno inventare canzoni, e non hanno la minima idea di quale sia la chiave o quale tipo di metro stiano usando.

SIMPLICIO:      Ma la matematica non è diversa? La matematica non è un linguaggio a parte, con simboli particolari che devono essere appresi prima di poter essere utilizzati?

SALVIATI:        Niente affatto. La matematica non è un linguaggio, è un’avventura. I musicisti “parlano forse un altro linguaggio” semplicemente perché hanno scelto di sintetizzare le loro idee con quei piccoli pallini neri? Anche se è così, questo non crea alcun ostacolo al bimbetto e alle sue canzoncine. Sì, una certa quantità di abbreviazioni matematiche si è evoluta nel corso dei secoli, ma ciò non è in alcun modo essenziale. La maggior parte della matematica si fa con un amico davanti ad una tazza di caffè, con un diagramma scarabocchiato su un tovagliolo. La matematica è ed è sempre stata una questione di idee, e le idee che contano trascendono i simboli con cui si sceglie di rappresentarle. Come Gauss fece notare una volta, “Ciò che ci serve sono le nozioni, non le notazioni”.

SIMPLICIO:      Ma non è forse uno degli obiettivi dell’educazione matematica aiutare gli studenti a pensare in un modo più preciso e più logico, e a sviluppare le loro “abilità razionali quantitative?” Non aprono forse la mente dei nostri studenti tutte queste definizioni e tutte queste formule?

SALVIATI:        No. Se mai, l’attuale sistema sortisce l’effetto opposto di rendere ottusa la mente. L’acume mentale di qualunque tipo deriva dalla risoluzione autonoma di problemi, non dal ricevere indicazioni su come risolverli.

SIMPLICIO:      D’accordo. Ma che cosa ne facciamo di quegli studenti che sono interessati ad intraprendere una carriera nell’ambito delle scienze o dell’ingegneria? Non servirà loro l’allenamento che il curriculum tradizionale mette a disposizione? Non è questo il motivo per cui si insegna matematica a scuola?

SALVIATI:        Quanti studenti che frequentano le lezioni di letteratura diventeranno un giorno scrittori? Questo non è il motivo per cui si insegna letteratura, e nemmeno quello per cui i ragazzi ne frequentano le lezioni. Si insegna per illuminare ciascuno, non solo per allenare futuri professionisti. In ogni caso, la migliore qualità per uno scienziato o per un ingegnere è essere in grado di pensare in modo creativo e autonomo. L’ultima cosa di cui ciascuno ha bisogno è di essere addestrato.

 

Il Curriculum di Matematica

L’aspetto veramente doloroso del modo in cui si insegna la matematica a scuola non è ciò che manca – il fatto che non c’è alcuna vera matematica nelle nostre lezioni di matematica – ma quello che c’è al suo posto: un mucchio confuso di disinformazione noto come “il curriculum di matematica”. Ora è giunto il momento di dare un’occhiata più da vicino a ciò a cui sono messi di fronte esattamente i nostri studenti – a che cosa vengono esposti in nome della matematica, e come vengono in questo danneggiati.

La cosa più impressionante del cosiddetto curriculum di matematica è la sua rigidità. Ciò è particolarmente vero nelle ultime classi. Da scuola a scuola, da città a città e da stato a stato, si sono dette e si sono fatte le stesse cose nello stesso identico modo e nello stesso identico ordine. Ben lungi dall’essere disturbati e contrariati da questo orwelliano stato di cose, la maggior parte della gente ha semplicemente accettato questo “modello standard” di curriculum matematico come sinonimo della matematica stessa.

Questo è intimamente connesso con ciò che io chiamo “il mito della scala a pioli” – l’idea che la matematica possa essere trattata come una sequenza di “argomenti” ciascuno dei quali sarebbe in qualche modo più avanzato o più elevato del precedente. Il risultato è quello di trasformare la matematica scolastica in una gara – alcuni studenti sono “in testa” rispetto ad altri, e i genitori si preoccupano se il loro figlio sta “rimanendo indietro”. E dove conduce esattamente questa gara? Che cosa li attende al traguardo? È una triste corsa che non porta da nessuna parte. Alla fine si è stati defraudati dell’istruzione matematica, e non la si conosce nemmeno.

La vera matematica non si presenta preconfezionata – non esiste qualcosa come un’idea di Algebra II. I problemi ti portano dove vogliono loro. L’arte non è una gara. Il mito della scala a pioli è una falsa immagine della materia, e il personale percorso degli insegnanti lungo il curriculum standard rinforza questo mito e impedisce loro di vedere la matematica come un tutto organico. Come risultato, abbiamo un curriculum di matematica senza prospettiva storica o coerenza tematica, una raccolta frammentaria di argomenti e regole assortiti, accomunati dal livello di difficoltà a cui possono essere ridotti da procedure graduali.

Al posto della scoperta e dell’esplorazione, abbiamo norme e regole. Non si sente mai nessuno studente che dica: “voglio vedere se ha senso innalzare un numero a una potenza negativa, e scopro che si ottiene una regolarità veramente splendida se si sceglie di usare questo sistema per indicare il reciproco di una potenza positiva”. Invece abbiamo insegnanti e libri di testo che presentano la “regola dell’esponente negativo” come un dato di fatto senza alcun accenno di estetica dietro questa scelta, o persino al fatto che sia una scelta.

Al posto di problemi significativi, che possono condurre a una sintesi di diverse idee, a territori inesplorati di discussione e di dibattito, e a un senso di unità tematica e di armonia nella matematica, si hanno esercizi tristi e ridondanti, specifici della tecnica in oggetto, e così disgiunti l’uno dall’altro e dalla matematica nel suo complesso che né gli studenti né i loro insegnanti hanno la più vaga idea del come o del perché una cosa del genere potrebbe aver avuto inizio.

Al posto di un naturale contesto problematico in cui possano prendere decisioni su quello che vogliono che le loro parole significhino, e su quali nozioni vorrebbero codificare, gli studenti sono sottoposti ad una sequenza interminabile di immotivate “definizioni” a priori. Il curriculum è ossessionato dal linguaggio settoriale e dalla nomenclatura, apparentemente per nessun altro proposito che quello di fornire agli insegnanti qualcosa su cui mettere alla prova gli studenti. Nessun matematico al mondo si prenderebbe la briga di fare queste insensate distinzioni: 2 1/2 è un “numero misto”, mentre 5/2 è una “frazione impropria”. Essi sono uguali per dirla tutta, forte e chiara. Sono gli stessi esatti numeri, e hanno esattamente le stesse proprietà. Chi usa tali termini al di fuori della classe quarta?

Naturalmente è molto più facile verificare la conoscenza di qualcuno su una definizione insensata piuttosto che ispirarlo a creare qualcosa di bello e a trovarne il significato. Anche se siamo d’accordo che un vocabolario di base per la matematica è importante, non è questo. Com’è triste che agli studenti del quint’anno si insegni a dire “quadrilatero” invece di “figura con quattro lati”, mentre non si è mai spiegato loro un motivo per utilizzare parole come “congettura” e “controesempio”. Gli studenti della scuola superiore devono imparare ad usare la funzione secante, “sec x” come un’abbreviazione per il reciproco della funzione coseno, “1 / cos x”, (una definizione con un peso intellettuale pari al peso della decisione di usare ”&” al posto di “e”). Che questa particolare abbreviazione, un’eredità delle tavole nautiche del XV secolo, sia ancora in uso (mentre altre, come il “verseno”, sono andate perdute) è un puro accidente storico, ed è del tutto senza valore in un’epoca in cui il calcolo nautico rapido e preciso non è più un problema. Sicché noi ingombriamo le nostre lezioni di matematica con nomenclatura insensata in un modo fine che è a se stesso.

In pratica, il curriculum non è tanto una sequenza di argomenti, o idee, quanto una sequenza di notazioni. Apparentemente la matematica consiste in una segreta lista di simboli mistici e di regole per la loro manipolazione. I bambini conoscono il segno “+” e il segno”-“. Soltanto più tardi sono introdotti alla “√”, e poi a “x” e “y” e all’alchimia delle parentesi. Infine, sono indottrinati sull’uso di “sen”, “log”, “f(x)”, e se sono molto bravi, “d” e “∫”. Il tutto senza aver avuto una sola significativa esperienza matematica.

Questo programma è così rigidamente definito che gli insegnanti e gli autori di libri di testo possono ragionevolmente prevedere, con anni di anticipo, che cosa precisamente faranno gli studenti, fino all’ultimo dettaglio degli esercizi. Non è del tutto inusuale trovare studenti del second’anno di Algebra a cui si chiede di calcolare [f(x+h)-f(x)] / h per varie funzioni f, in modo tale che l’avranno “visto” quando studieranno l’analisi matematica qualche anno dopo. Naturalmente non viene data alcuna motivazione (e neppure è attesa) sul perché una tale combinazione apparentemente casuale di operazioni sarebbe di qualche interesse, sebbene io sia convinto che ci siano molti insegnanti che cercano di spiegare che cosa significhi un’operazione come questa, e penso che stiano facendo un favore ai loro studenti, anche se in realtà per questi è soltanto un ulteriore noioso problema di matematica da risolvere. “Che cosa vogliono che faccia? Oh, soltanto applicare questa tecnica? OK.”

Un altro esempio è l’allenamento degli studenti per esprimere informazioni in una forma inutilmente complicata, semplicemente perché in qualche lontano futuro ciò avrà un senso. Qualunque insegnante di algebra della scuola media ha almeno una vaga idea del motivo per cui chiede ai suoi studenti di riformulare “il numero x è compreso tra tre e sette” come | x-5 | < 2? Gli autori di questi libri di testo, inetti senza speranza, credono davvero di aiutare gli studenti a prepararsi per un giorno, che forse verrà tra qualche anno, quando potrebbero dover operare all’interno di una geometria pluridimensionale o in uno spazio metrico astratto? Ne dubito. Penso che si stiano copiando l’un l’altro decenni dopo decenni, forse cambiando i caratteri o i colori dei titoli, e riempiendosi d’orgoglio quando un sistema scolastico adotta i loro libri, e diventa loro inconsapevole complice.

La matematica si occupa di problemi, e i problemi devono diventare il centro della vita matematica di ciascuno studente. Per quanto dolorosi e creativamente frustranti possano essere i problemi, gli studenti e i loro insegnanti dovrebbero essere sempre impegnati nel processo: comprendere, non comprendere, scoprire schemi, fare congetture, costruire esempi e controesempi, escogitare dimostrazioni, ed esaminare criticamente a vicenda il proprio lavoro. Tecniche specifiche e metodi scaturiranno in modo naturale dal processo, come è sempre avvenuto nella storia: non isolati dal loro problema di sfondo, ma organicamente connessi ad esso, e da esso risultanti.

Gli insegnanti di inglese sanno che l’ortografia e la pronuncia si apprendono meglio in un contesto di lettura e scrittura. Gli insegnanti di storia sanno che i nomi e le date perdono il loro significato se decontestualizzati dai fatti storici di riferimento. Perché l’istruzione matematica rimane bloccata al diciannovesimo secolo? Confrontate la vostra personale esperienza dell’apprendimento dell’algebra con la descrizione di Bertrand Russell:

“Ero obbligato a imparare a memoria: “il quadrato della somma di due numeri è uguale alla somma dei loro quadrati aumentati del doppio del loro prodotto”. Non avevo la più vaga idea di che cosa ciò significasse e quando non riuscivo a ricordarmi le parole, il mio maestro mi lanciava il libro sulla testa, il che non stimolava in alcun modo la mia intelligenza”.

Le cose sono davvero diverse oggi?

SIMPLICIO:      Non penso che questo sia molto corretto. Sicuramente i metodi di insegnamento si sono evoluti da allora.

SALVIATI:        Ti riferisci ai metodi di addestramento. Insegnare è una relazione umana complicata; non richiede un metodo. O piuttosto dovrei dire, se hai bisogno di un metodo probabilmente non sei un buon insegnante. Se non hai abbastanza feeling con la tua materia da essere in grado di esprimerti con una voce personale, in un modo naturale e spontaneo, come potresti capirla? E a proposito di essere fermi al diciannovesimo secolo, non è scioccante come il curriculum stesso sia fermo al diciassettesimo? Pensa a tutte le belle scoperte e alle profonde rivoluzioni nel pensiero matematico che sono avvenute negli ultimi tre secoli! Non c’è alcun accenno ad esse, come se non fossero mai esistite.

SIMPLICIO:      Ma non stai pretendendo davvero troppo dai nostri insegnanti di matematica? Ti aspetti che prestino un’attenzione individuale a dozzine di studenti, che li guidino ciascuno sulla propria strada verso la scoperta e l’illuminazione, e che siano aggiornati anche sulla storia della matematica recente?

SALVIATI:        Ti aspetti che il tuo insegnante di arte sia in grado di darti consigli personalizzati e competenti sulla tua pittura? Ti aspetti che sappia tutto della storia dell’arte degli ultimi trecento anni? Sul serio, non mi aspetto nulla nel genere, vorrei soltanto che fosse così.

SIMPLICIO:      Sei così critico nei confronti degli insegnanti di matematica?

SALVIATI:        No, biasimo solo la cultura che li produce. Quei poveri diavoli stanno facendo del loro meglio, e stanno facendo ciò per cui sono stati addestrati. Sono sicuro che molti di loro amano i loro studenti e odiano ciò che sono costretti a propinare. Sanno in cuor loro che è senza senso e degradante. Sentono di essere stati trasformati in ingranaggi di una grande macchina tritura-anime, ma non hanno la larghezza di prospettiva necessaria per comprendere tutto questo, o per combatterlo. Sanno soltanto che devono “preparare gli studenti per l’anno successivo”.

SIMPLICIO:      Pensi davvero che la maggior parte degli studenti sia capace di operare ad un livello così alto da creare la propria matematica personalizzata?

SALVIATI:        Se, in tutta onestà, crediamo che il ragionamento creativo sia troppo “elevato” per i nostri studenti, e che non sappiano utilizzarlo, perché permettiamo loro di scrivere dissertazioni di storia o saggi su Shakespeare? Il problema non è che gli studenti non sono in grado di utilizzarlo, è che nessuno degli insegnanti è in grado di farlo. Non si sono mai messi alla prova, perciò come potrebbero guidare uno studente? In ogni caso, ci sarebbe ovviamente una differenziazione dell’interesse e dell’abilità dello studente, come avviene in qualunque materia, ma almeno gli studenti amerebbero o odierebbero la matematica per ciò che è veramente, e non per questa perversa parodia che ne viene fatta.

SIMPLICIO:      Ma certamente vogliamo che tutti i nostri studenti apprendano un repertorio di base di fatti e abilità. Questo è ciò a cui serve il curriculum, ed è per questo motivo che è così uniforme – ci sono certi fatti senza tempo, fatti nudi e crudi che è necessario far imparare ai nostri studenti: uno più uno uguale a due, e la somma degli angoli interni di un triangolo è 180 gradi. Queste non sono opinioni, o sdolcinate sensazioni artistiche.

SALVIATI:        Al contrario. Le strutture matematiche, utili o no, sono inventate e sviluppate nel contesto di un problema, e ricavano il loro significato dal contesto. Qualche volta vogliamo che uno più uno sia uguale a zero (come nella cosiddetta aritmetica “mod 2”) e sulla superficie di una sfera la somma degli angoli di un triangolo misura più di 180 gradi. Non ci sono “fatti” in sé; ogni cosa è relativa e relazionale. È la storia che importa, non soltanto il finale.

SIMPLICIO:      Mi sto stancando di tutto questo mistico mumbo-jumbo! Aritmetica di base, va bene? Sei d’accordo o no che gli studenti la dovrebbero imparare?

SALVIATI:        Dipende da che cosa intendi con “la” aritmetica. Se intendi di avere un interesse per il problema del contare e del classificare, i vantaggi di raggruppare e catalogare, la distinzione tra la rappresentazione e la cosa in sé, e alcune idee dello sviluppo storico dei sistemi numerici, allora sì, penso che i nostri studenti dovrebbero essere esposti a tali cose. Se intendi la meccanica memorizzazione di fatti aritmetici senza alcuna cornice concettuale sottostante, allora no. Se intendi analizzare i fatti niente affatto ovvi che cinque gruppi di sette sono la stessa cosa di sette gruppi di cinque, allora sì. Se intendi creare la regola secondo cui 5x7 = 7x5, allora no. Fare matematica dovrebbe sempre voler dire scoprire schemi e costruire spiegazioni belle e significative.

SIMPLICIO:      E la geometria? Non sperimentano le cose con la geometria? Non è forse vero che la Geometria della Scuola Superiore è un esempio perfetto di ciò che vorresti che fossero le lezioni di matematica?

 

La Geometria della Scuola Superiore: strumento del diavolo

 

Non c’è niente di più irritante per l’autore della feroce accusa di aver offerto il suo sostegno al principale bersaglio del suo veleno. E non c’è mai stato un lupo travestito da agnello tanto insidioso, e nemmeno un falso amico così pericoloso, della Geometria della Scuola Superiore. E questo precisamente perché è lo sforzo della scuola di introdurre gli studenti all’arte della dimostrazione che la rende così pericolosa.

Ponendosi come l’arena in cui gli studenti alla fine si incontreranno con il vero ragionamento matematico, questo virus attacca la matematica al suo cuore, distruggendo la profonda essenza del ragionamento creativo razionale, avvelenando il piacere degli studenti per questa materia affascinante e bella, e rendendoli permanentemente inabili a pensare la matematica in un modo naturale e intuitivo.

Il meccanismo sotteso a ciò è sottile e deviante. Lo studente-vittima è dapprima stordito e paralizzato da un furibondo attacco di precisissime definizioni, teoremi, e simboli, e poi lentamente e diligentemente viene distolto da ogni naturale curiosità o intuizione sulle forme e sui loro schemi da un indottrinamento sistematico nel linguaggio artefatto e nel modello artificiale della cosiddetta ”dimostrazione geometrica formale”.

Al di là di ogni metafora, la lezione di geometria è di gran lunga la componente più distruttiva sotto il profilo mentale ed emozionale dell’intero curriculum di matematica K-12. Gli altri corsi di matematica possono nascondere l’uccello meraviglioso, o metterlo in una gabbia, ma nella lezione di geometria, esso viene palesemente e crudelmente torturato. (A quanto pare sono incapace di lasciar da parte le metafore).

Quello che sta succedendo è il sistematico scardinamento dell’intuizione dello studente. Una dimostrazione, cioè, un’argomentazione matematica, è un lavoro di invenzione, una poesia. Il suo scopo è soddisfare. Una bella dimostrazione dovrebbe spiegare, e dovrebbe spiegare chiaramente, in profondità e con eleganza. Una dimostrazione ben scritta e ben articolata dovrebbe fare l’effetto di uno spruzzo di acqua fresca, ed essere un raggio di luce – dovrebbe rinfrescare lo spirito e illuminare la mente. E dovrebbe essere affascinante.

Non c’è niente di affascinante in ciò che viene fatto passare come dimostrazione in una lezione di geometria. Agli studenti viene presentato un modello precostituito rigido e dogmatico a cui devono essere ricondotte le loro cosiddette “dimostrazioni” – un modello precostituito tanto inutile e inappropriato quanto l’insistere perché dei bambini che vogliono coltivare un giardino facciano riferimento ai loro fiori considerandone il genere e la specie.

 

Diamo un’occhiata a qualche specifico esempio di questa follia. Cominceremo con l’esempio di due rette che si incrociano:

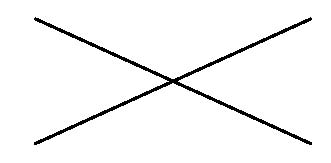
Ora la prima cosa che di solito succede è l’inutile intorbidamento delle acque con simboli eccessivi. Pare che non si possa parlare semplicemente di due linee rette incrociate; si devono dare loro dei nomi elaborati. E non nomi semplici come “retta 1” e “retta 2”, o persino “a” e “b”. Dobbiamo (secondo la Geometria della Scuola Superiore) selezionare punti casuali e irrilevanti su queste rette, e poi fare riferimento alle rette usando la speciale “simbologia delle linee”

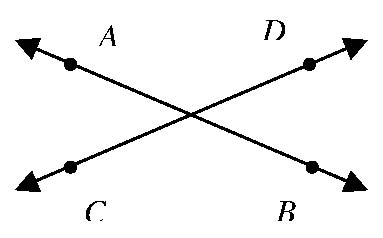
Vedete, ora dobbiamo chiamarle . E, sia chiaro!, dovete tralasciare i trattini in alto – “” si riferisce alla lunghezza della linea AB (almeno penso che funzioni così). Non importa quanto sia inutilmente complicato, questo è il modo in cui si deve imparare a farlo. Ora ecco il vero e proprio enunciato, a cui di solito ci si riferisce con un nome assurdo come

PROPOSIZIONE 2.1.1

Siano AB e CD due rette che si intersecano in P. Allora ∠APC  @ ∠BPD (figura 2 pag. 19)

In altre parole, gli angoli dalle due parti sono uguali. Bene! La configurazione di due rette che si incrociano è simmetrica, accidenti. E come se questo non fosse già abbastanza negativo, questa affermazione palesemente ovvia sulle rette e sugli angoli deve essere “dimostrata”.

Enunciazione	Spiegazione
1.      m∠APC + m ∠APD = 180       m∠BPD + m∠APD = 180	1.      Additività della misura degli angoli
2.      m∠APC+m∠APD = m∠BPD + m∠APD	2.      Proprietà sostitutiva
3.      m∠APD= m∠APD	3.      Proprietà transitiva
4.      m∠APC= m∠BPD	4.   Primo principio di equivalenza1
5.      ∠APC = ∠BPD	5.      Postulato della misura degli angoli2

Al posto di un ragionamento acuto e ingegnoso scritto da un vero essere umano, e condotto in uno dei molteplici linguaggi naturali, noi abbiamo questo modello astioso, arido e burocratico di dimostrazione. E che montagna è diventato quel granello di sabbia! Vorreste davvero dire che un’osservazione così diretta come questa richieda un preambolo tanto lungo? Siate onesti: l’avete mai letta? Ovviamente no. Chi la vorrebbe leggere?

L’effetto di un lavoro di tal genere su qualcosa di così semplice è quello di far dubitare la gente della propria intuizione. Mettere in discussione l’ovvio, insistendo sul fatto che è “rigorosamente provato” (come se ciò che abbiamo detto sopra costituisse una dimostrazione formale legittima) è come dire a uno studente, “I tuoi sentimenti e le tue idee sono sospette. Devi pensare e parlare come noi”.

Ora c’è posto per le dimostrazioni formali in matematica, senza dubbio. Ma quel posto non è la prima introduzione di uno studente alla dimostrazione matematica. Almeno lasciamo che le persone prendano familiarità con alcuni oggetti matematici, e imparino che cosa aspettarsi da essi, prima di cominciare a formalizzare tutto. Le dimostrazioni formali rigorose diventano importanti solo quando c’è una crisi – quando scopri che il tuo oggetto immaginario si comporta in senso opposto alle tue intuizioni; quando c’è un paradosso di qualche genere. Ma un’igiene preventiva così spropositata è completamente inutile qui – non si è ancora ammalato nessuno! Naturalmente se dovesse manifestarsi qualche crisi logica ad un certo punto, allora ovviamente dovremmo indagarla, e dovremmo rendere più chiara la dimostrazione, ma quel processo può essere portato avanti anche intuitivamente e informalmente. In effetti è l’anima della matematica far progredire un tale dialogo con le proprie dimostrazioni.

Così, non soltanto la maggior parte dei ragazzi è completamente confusa da questa pedanteria – niente è più mistificante di una dimostrazione dell’ovvio – ma persino quei pochi che hanno conservato intatta la loro intuizione devono ritradurre le loro idee belle ed eccellenti in questa cornice geroglifica per far sì che i loro insegnanti la ritengano “corretta”. L’insegnante allora si illude di rendere acuta in qualche misura la mente dei suoi studenti.

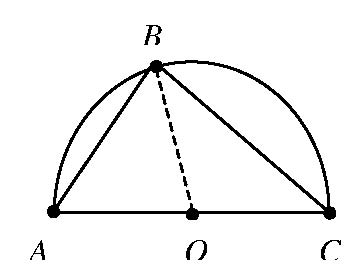
Come esempio più serio, prendiamo il caso di un triangolo inscritto in una semicirconferenza:

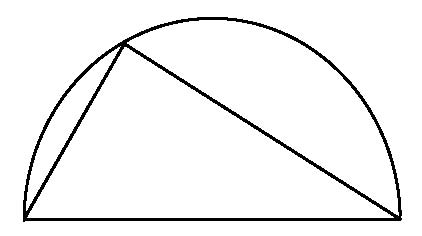
Ora la bella verità di questo schema è che indipendentemente dal punto sulla circonferenza in cui si posiziona il vertice del triangolo, esso formerà sempre un bell’angolo retto. (Non ho obiezioni a un termine quale “angolo retto” se è importante per il problema e lo rende più facile da discutere. Non è la terminologia ciò a cui obietto, è alla terminologia completamente inutile. In ogni caso, sarei felice di utilizzare il termine “corner” o persino “porcile” se uno studente lo preferisse).

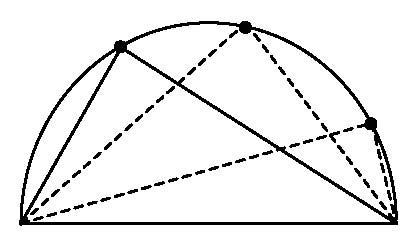
Ecco un caso in cui la nostra intuizione è in qualche misura messa in dubbio. Non è del tutto chiaro che questo sia vero; sembra persino che non sia così – non dovrebbe cambiare l’angolo se sposto il suo vertice? Quello che abbiamo qui è un fantastico problema di matematica! È vero? Se lo è, perché è vero? Che grandioso progetto! Che fantastica opportunità di esercitare la propria ingenuità e la propria immaginazione! Naturalmente ai nostri studenti non viene data alcuna opportunità di tal genere, e così la loro curiosità e il loro interesse sono immediatamente appiattiti da:

TEOREMA 9.5. Sia ΔABC inscritto in una semicirconferenza con diametro AC. Allora ∠ABC è un angolo retto.

Dimostrazione:

Enunciazione	Spiegazione
1.     Disegna il raggio OB. Allora OB=OC=OA	1.      Dato
2.  m∠OBC=m∠BCA       m∠OBA=m∠BAC	2.      Teorema del triangolo isoscele
3.  m∠ABC=m∠OBA+m∠OBC	3.      Additività della misura degli angoli
4.  m∠ABC+m∠BCA+m∠BAC=180	4.      La somma degli angoli di un triangolo è 180
5.  m∠ABC+m∠OBC+m∠OBA=180	5.      Sostituzione (riga 2)
6.  2m∠BC=180	6.      Sostituzione (riga 3)
7. m∠ABC=90	7.      (Secondo) Principio di equivalenza3
8.     ∠ABC è un angolo retto	8.      Definizione di angolo retto

 

Può esserci qualcosa di meno attraente ed elegante? Può una dimostrazione essere più confusa e illeggibile? Questa non è matematica! Una dimostrazione dovrebbe essere un’epifania di Dio, non un messaggio in codice dal Pentagono. Questo è ciò che deriva da un errato senso del rigore logico: la bruttezza. Lo spirito della dimostrazione è stato seppellito sotto un cumulo di confuso formalismo.

Nessun matematico lavora in questo modo. Nessun matematico ha mai lavorato in questo modo. Questo è un fraintendimento totale e profondo della sfida matematica. La matematica non consiste nell’erigere barriere tra noi stessi e la nostra intuizione, e rendere complicate le cose semplici. Confrontate questa ributtante confusione di dimostrazione con il seguente ragionamento logico concepito da uno dei miei studenti del settimo anno:

“Prendete il triangolo e ruotatelo in modo che formi un quadrilatero inscritto nel cerchio. Dato che il triangolo ruota completamente, i lati del quadrilatero devono essere paralleli, perciò esso forma un parallelogramma. Ma non può essere un quadrilatero con i lati obliqui perché entrambe le sue diagonali sono diametri del cerchio, perciò sono uguali, il che significa che deve essere proprio un rettangolo. Questo è il motivo per cui l’angolo è sempre un angolo retto”.

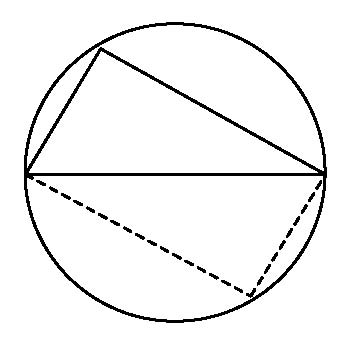
Non è semplicemente delizioso? E il punto non è se questa dimostrazione è migliore di un’altra come idea, il punto è che nell’idea ci si imbatte. (In effetti l’idea della prima dimostrazione è abbastanza bella, benché si veda come attraverso un vetro, oscurata).

Cosa più importante, l’idea era originale dello studente. La classe aveva un bel problema su cui lavorare, sono state fatte delle congetture, sono state tentate delle dimostrazioni, e questa è una di quelle a cui è approdato uno studente. Naturalmente ci sono voluti parecchi giorni, ed è stato il risultato finale di una lunga serie di fallimenti.

Ad essere sincero, ho parafrasato notevolmente la dimostrazione. Quella originale era un po’ più contorta e conteneva un sacco di parole non necessarie (ed anche errori di ortografia e grammatica). Ma penso di essere riuscito a comunicarne il senso. E questi difetti erano tutti a fin di bene; mi hanno dato qualcosa da fare come insegnante. Sono riuscito ad evidenziare parecchi problemi logici e di stile, e lo studente allora è stato in grado di migliorare la sua dimostrazione. Per esempio, non ero del tutto contento del pezzo su entrambe le diagonali che sono diametri – non pensavo che fosse del tutto ovvio – ma ciò significava soltanto che c’era ancora tanto da pensare e da capire dalla situazione. E infatti lo studente è stato capace di colmare abbastanza bene la lacuna:

“Dato che il triangolo è stato ruotato per metà attorno al cerchio, il vertice deve finire esattamente al punto opposto a quello da cui era partito. Questo è il motivo per cui l’altra diagonale del rettangolo è un diametro”.

Così abbiamo un grande progetto e un bel pezzo di matematica. Non so chi ne sia stato più orgoglioso, se lo studente o io stesso. Questo è esattamente il tipo di esperienza che voglio che i miei studenti facciano.

Il problema del curriculum standard di geometria è che l’esperienza privata e personale di essere un artista che lotta è stata virtualmente eliminata. L’arte della dimostrazione è stata rimpiazzata da una rigida struttura graduata di deduzioni formali senza alcuna ispirazione. Il libro di testo presenta un insieme di definizioni, teoremi e dimostrazioni, gli insegnanti li copiano alla lavagna, e gli studenti li copiano sui loro quaderni. Poi si richiede loro di imitarli negli esercizi. Quelli che imparano velocemente il metodo sono “bravi” studenti.

Il risultato è che lo studente diventa il membro passivo di un atto creativo. Gli studenti formulano affermazioni che si adattano a preesistenti schemi di dimostrazione, non perché sanno ciò che vogliono dire. Sono addestrati a scimmiottare le dimostrazioni, non a comprenderle. Così non solo non hanno la minima idea di ciò che i loro insegnanti vanno dicendo, anche loro non hanno idea di ciò che essi stessi dicono.

Persino il modo tradizionale in cui le definizioni sono presentate è una menzogna. In uno sforzo di creare un’illusione di “chiarezza” prima di imbarcarsi nella tipica cascata di proposizioni e teoremi, viene fornita una serie di definizioni in modo tale che le enunciazioni e le relative dimostrazioni possano essere il più possibile sintetiche. In apparenza ciò sembra abbastanza innocuo; perché non ricorrere ad alcune abbreviazioni in maniera tale che si possano dire le cose in modo più economico? Il problema è che le definizioni hanno una loro importanza. Esse discendono da decisioni estetiche su quali distinzioni tu come artista consideri importanti. Ed esse sono generate dai problemi. Elaborare una definizione è portare all’evidenza e richiamare l’attenzione su un elemento o su una proprietà strutturale. Dal punto di vista storico ciò segue il lavoro su di un problema, non è un preludio ad esso.

Il punto è che non si parte con le definizioni, si parte con i problemi. Nessuno ha mai avuto l’idea che un numero fosse “irrazionale” fino a che Pitagora non cercò di misurare la diagonale di un quadrato e scoprì che non poteva essere rappresentata come frazione. Le definizioni hanno senso quando in una dimostrazione si raggiunge un punto che rende necessaria la distinzione. Elaborare definizioni senza motivazione crea, con elevata probabilità, confusione. Questo è ancora un altro esempio del modo in cui gli studenti sono protetti ed esclusi dal processo matematico. Gli studenti hanno bisogno di elaborare le loro definizioni quando si presenta la necessità, per gestire da soli la discussione. Non voglio che gli studenti dicano “la definizione, il teorema, la dimostrazione”, voglio che dicano, “la mia definizione, il mio teorema, la mia dimostrazione”.

A parte tutte queste lamentele, il vero problema di questo tipo di presentazione è che è noiosa. Efficienza ed economia da sole non fanno una buona pedagogia. Stento a credere che Euclide approverebbe ciò; so che Archimede non lo farebbe.

SIMPLICIO:      Ora aspetta un minuto. Non so tu, ma a me piacevano davvero le mie lezioni di geometria alla scuola superiore. Mi piaceva l’impostazione, e mi piaceva lavorare all’interno del rigido formato della dimostrazione.

SALVIATI:        Sono sicuro che ti piacevano. Probabilmente hai avuto anche l’occasione di lavorare su alcuni simpatici problemi. A molte persone piacciono le lezioni di geometria (anche se molti di più le odiano). Ma questo non è un punto a favore dell’attuale regime. Piuttosto, esso è la potente testimonianza del fascino della matematica stessa. È difficile mandare completamente in rovina qualcosa di così bello; persino questa ombra diafana di matematica può ancora essere coinvolgente e soddisfacente. Molte persone si divertono allo stesso modo anche con la pittura-con-i-numeri; è un’attività manuale rilassante e colorata. Questo non la trasforma nella cosa reale.

SIMPLICIO:      Ma ti sto dicendo che mi piaceva.

SALVIATI:        E se avessi fatto una maggior esperienza della matematica naturale, ti sarebbe piaciuta anche di più.

SIMPLICIO:      Così dovremmo soltanto partire per qualche escursione di matematica in libertà, e gli studenti impareranno qualunque cosa gli capiti di imparare?

SALVIATI:        Precisamente. I problemi conducono ad altri problemi, le tecniche si svilupperanno quando saranno necessarie, e nuovi argomenti emergeranno in modo naturale. E se accadrà che qualche argomento non venga mai alla luce in tredici anni di scolarizzazione, perché mai dovrebbe essere interessante o importante?

SIMPLICIO:      Sei completamente impazzito.

SALVIATI:        Forse sì. Ma anche seguendo il programma convenzionale un buon insegnante può guidare la discussione e il flusso dei problemi così da permettere agli studenti di scoprire e inventare la matematica da sé. Il problema vero è che la burocrazia non permette al singolo insegnante di farlo. Con un curriculum predeterminato da seguire, un insegnante non può essere autonomo. Non ci dovrebbero essere né regole né curriculum. Solo individui che fanno ciò che credono meglio per i loro studenti.

SIMPLICIO:      Ma allora come fanno le scuole a garantire che i loro studenti abbiano tutti la stessa preparazione di base? Come faranno a misurare accuratamente il loro valore relativo?

SALVIATI:        Non possono e non lo faranno. Proprio come nella vita reale. In ultima istanza devi rassegnarti di fronte al fatto che le persone sono tutte diverse, e questo è soltanto positivo. In ogni caso, non c’è urgenza. Così una persona si diploma alla scuola superiore senza sapere le formule per dimezzare gli angoli (come se le sapessero ora!) E allora? Almeno quella persona si sarà fatta una qualche idea di ciò in cui la materia consiste veramente, e avrà visto qualcosa di bello.

 

In conclusione…

Per dare il tocco finale alla mia critica sul curriculum standard, e come servizio alla comunità, presento ora il programma, per la prima volta completamente onesto, per la matematica K-12.

Il Curriculum Standard di Matematica per la Scuola

MATEMATICA ALLA SCUOLA INFERIORE. Comincia l’indottrinamento. Gli studenti imparano che la matematica non è qualcosa che si fa, ma qualcosa che viene fatto a te. L’enfasi è posta sullo stare seduti fermi, riempire fogli, e seguire direttive. Ai bambini si richiede di saper padroneggiare una serie complessa di algoritmi per manipolare simboli indiani, scollegati da qualunque reale desiderio o curiosità da parte loro, e considerati soltanto pochi secoli fa troppo difficili anche per un adulto medio. Grande enfasi viene data alle tabelle di moltiplicazioni, tanto che i genitori, gli insegnanti, e i bambini stessi sono stressati [gioco di parole con stress che in inglese significa sia enfatizzato che stressato psicologicamente, N.d.T.].

MATEMATICA ALLA SCUOLA MEDIA. Agli studenti viene insegnato a vedere la matematica come una serie di procedure, simili a riti religiosi, che sono eterni e scolpiti nella pietra. Le sacre tavole, o “Libri di Matematica”, sono esposte, e gli studenti imparano a dare del “Loro” ai capi più anziani della chiesa (come nelle frasi “Che cosa vogliono qui?” “Vogliono che io divida?”). Saranno introdotti “word problem” artefatti ed artificiali tanto da far sembrare a confronto divertente il faticoso lavoro insensato dell’aritmetica. Gli studenti saranno sottoposti a verifica su un’ampia gamma di inutili termini tecnici, come “numero intero” e “frazione propria”, senza la minima motivazione per operare tali distinzioni. Eccellente preparazione per Algebra I.

ALGEBRA I. Per non perdere tempo prezioso a pensare ai numeri e ai loro schemi, questo corso concentra invece la sua attenzione sui simboli e sulle regole per la loro manipolazione. Lo scorrevole flusso narrativo che va dai problemi sulle tavolette degli antichi popoli mesopotamici all’arte elevata degli esperti di algebra del Rinascimento è scartato in favore di una fastidiosa riproposizione frammentaria postmoderna di un racconto senza personaggi, trama o tema. L’insistenza che tutti i numeri e le espressioni si presentino in varie forme predefinite procurerà ancora più confusione sul significato di identità e di uguaglianza. Gli studenti devono anche memorizzare la formula delle equazioni di secondo grado per non ben precisati motivi.

GEOMETRIA. Isolata dal resto del curriculum, questo corso solleverà le speranze degli studenti che vogliono impegnarsi in una attività matematica che abbia senso, e poi le abbatterà. Sarà introdotta una simbologia rozza e fuorviante, e non sarà risparmiato alcuno sforzo per far sembrare complicato ciò che è semplice. L’obiettivo di questo corso è quello di sradicare qualunque impronta residua di naturale intuizione matematica, in preparazione ad ALGEBRA II.

ALGEBRA II. L’argomento di questo corso è l’uso immotivato e inappropriato della geometria analitica. Le sezioni coniche sono inserite in un sistema di coordinate così da evitare la semplicità estetica dei coni e delle loro sezioni. Gli studenti impareranno a riscrivere forme quadratiche in una varietà di forme predefinite, senza alcun motivo. Anche le funzioni esponenziali e logaritmiche vengono introdotte nell’ALGEBRA II, nonostante non siano oggetti algebrici, semplicemente perché devono essere messi da qualche parte, a quanto pare. Il nome del corso è scelto per rinforzare la mitologia della scala a pioli. Perché la Geometria si posizioni tra l’Algebra I e la sua prosecuzione resta un mistero.

TRIGONOMETRIA. Due settimane di contenuti sono prolungate per la durata di un semestre da masturbatori giri di definizioni. A fenomeni veramente interessanti e belli, quali il modo in cui la misura dei lati di un triangolo dipenda dai suoi angoli, viene data la stessa enfasi che a irrilevanti abbreviazioni e obsolete convenzioni simboliche, in modo da impedire agli studenti di farsi una chiara idea di ciò in cui consiste la materia. Gli studenti impareranno trucchetti del tipo “SohCahToa” [acronimi per ricordarsi le leggi trigonometriche: SOH:Sine equals Opposite over Hypotenuse. CAH: Cosine equals Adjacent over Hypotenuse. TOA: Tangent equals Opposite over Adjacent, N.d.T.] invece di sviluppare una naturale sensibilità intuitiva per l’orientamento e la simmetria. La misura di angoli e lati dei triangoli sarà discussa senza far cenno alla natura trascendente delle funzioni trigonometriche, o i conseguenti problemi linguistici e filosofici relativi all’effettuare tali misurazioni. È richiesto l’uso delle calcolatrici, in modo da confondere ulteriormente questi argomenti.

PRE-ANALISI. Un insensato guazzabuglio di argomenti sconnessi. Prevalentemente un tentativo malriuscito di introdurre i metodi analitici del tardo diciannovesimo secolo in situazioni in cui non sono né necessari né utili. Le definizioni tecniche di “limiti” e “continuità” sono presentate per oscurare la nozione intuitivamente chiara di cambiamento uniforme. Come suggerisce il nome, questo corso prepara gli studenti per il corso di Analisi, in cui sarà completata la fase finale del sistematico offuscamento di qualsiasi idea naturale connessa alla forma e al movimento.

ANALISI. Questo corso esplorerà la matematica del movimento, e i modi migliori per seppellirla sotto una montagna di inutile formalismo. Nonostante esso sia un’introduzione tanto al calcolo differenziale quanto al calcolo integrale, le idee semplici e profonde di Newton e Leibniz saranno lasciate da parte in favore del più sofisticato approccio basato sulle funzioni, sviluppato in risposta alle varie crisi analitiche che non si applicano affatto a questo scenario, e che ovviamente non saranno menzionate. Pronto per essere ripreso al college, parola per parola.

*** 

Eccola qui. Una prescrizione completa per rendere permanentemente inabili le giovani menti – una cura efficace contro la curiosità. Ecco che cosa hanno fatto alla matematica!

C’è così tanta profondità da togliere il fiato e c’è una bellezza così commovente in questa antica forma d’arte. Com’è ironico che la gente abbandoni la matematica come antitesi della creatività. Stanno perdendo una forma d’arte più antica di qualunque libro, più profonda di qualsiasi poesia, e più astratta di qualunque astrazione. Ed è stata la scuola a fare questo! Che triste circolo vizioso di insegnanti innocenti che infliggono un danno a studenti innocenti. Potremmo tutti divertirci molto di più.

SIMPLICIO:      Bene, sono completamente depresso. E ora?

SALVIATI:        Beh, mi è venuta un’idea che riguarda una piramide inscritta in un cubo…

 

¹ Sommando o sottraendo a entrambi i membri di un`equazione uno stesso numero o una stessa espressione algebrica si ottiene un`equazione equivalente alla data (nota di XlaTangente)

² Angoli aventi la stessa ampiezza sono congruenti (nota di XlaTangente)

³ Moltiplicando o dividendo entrambi i membri di un` equazione per uno stesso numero diverso da zero si ottiene un'equazione equivalente all'equazione data (nota di XlaTangente)