Stella octangula

Vogliamo provare a costruire con Pov Ray una stella octangula; e per il momento vi diamo qui soltanto il primo passo. La stella octangula è una stella a otto punte, come quella che si vede qui sotto, costruita con stuzzicadenti e palline di plastilina. Si parte da un ottaedro regolare (i vertici dell’ottaedro sono le 6 palline rosse) e su ciascuna delle sue 8 facce si costruisce un tetraedro regolare, aggiungendo un solo vertice (le palline verdi) per ciascuna faccia.

Primo passo: l’ottaedro

Per disegnare poliedri una via possibile può essere quella di calcolare le coordinate dei vertici e poi unirli con gli spigoli opportuni e creare le facce necessarie. La costruzione che ci proponiamo di realizzare richiede la costruzione di un ottaedro. Sarà quindi utile iniziare il lavoro disegnandone uno. A seconda di come disponiamo l’ottaedro nello spazio le coordinate dei punti cambiano. Il suggerimento è di trovare una posizione semplice per scrivere rapidamente le coordinate e poi, se in realtà volevamo la figura in un altro 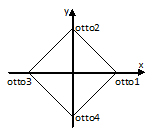modo, ruotarla, dilatarla, traslarla in seguito. Una scelta comoda può essere quella di disegnare l’ottaedro partendo da un quadrato centrale posto sul piano z=0 (i cui vertici corrispondono a 4 dei 6 vertici di un ottaedro). Gli ultimi due vertici verranno ottenuti con alcune considerazioni sui triangoli equilateri. Per avere maggiore simmetria e aiutarmi in seguito con i calcoli voglio costruire un quadrato che abbia centro nell’origine e con le diagonali sugli assi cartesiani. Scelgo quindi i punti otto1=(1,0), otto2=(0,1), otto3=(-1,0), otto4=(0,-1). Devo ricordarmi che i punti si trovano in uno spazio tridimensionale e che PovRay utilizza una terna sinistrorsa (per cui i punti sono indicati specificando (xp,zp,yp) ).

Ora che ho trovato i punti del quadrato mi rimangono solamente i punti ottosu ed ottogiu (i due punti rimanenti che non si trovano nel piano su cui giace il quadrato costruito prima) Per la simmetria dell’ottaedro posso ottenere un quadrato anche tagliando con un piano verticale, ottenendo quindi le coordinate dei punti ottosu e ottogiu.

Ora che ho ricavato i vertici dovrò rappresentarli con dei punti e poi unirli con degli spigoli. Useremo come punti delle sfere e come linee dei cilindri. Sarà utile memorizzare in due variabili i raggi dei cilindri e delle sfere in modo da poterli poi cambiare più velocemente. I punti uniti da linee saranno quelli del quadrato otto1otto2otto3otto4 (senza le diagonali però); il punto ottosu è collegato a tutti i punti del quadrato (ma non al punto ottogiu) e il punto ottogiu è collegato a tutti i punti del quadrato (ma non al punto ottosu). Il totale sarà di 6 punti e 12 linee.

E il resto alla prossima puntata… Per suggerimenti, consigli, domande saremo ben felici di rispondervi all'indirizzo: officina@xlatangente.it

ottaedro